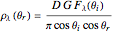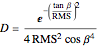Comparing the Cook-Torrance BRDF Model with Diffuse Reflection Simulation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
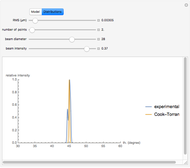
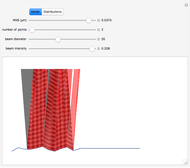
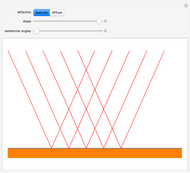
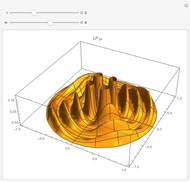
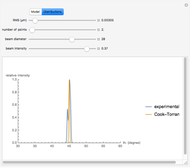
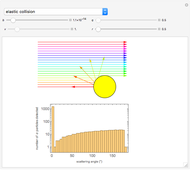
As Wolfgang Pauli said, “God made the bulk; the surface was invented by the devil.” This Demonstration illustrates the diabolical characteristics of surfaces in the case of reflection. In this specific case, we show how reflection is affected by surface roughness. The latter is described by means of the root mean square (RMS) average of profile height deviations from the mean, recorded within the evaluation length. On smooth surfaces, light is reflected according to Snell's law, in terms of the angle between the incident ray and the surface normal. This law also applies in the case of rough surfaces; however, the inclination of each facet now needs to be accounted for. This gives rise to complications, such as interferences, multiple reflections, etc. We have analyzed only the diffuse reflection, which applies when the wavelength is much greater than RMS (Rayleigh criterion [1]). The incident angle 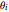 has been set to 45 degrees.
has been set to 45 degrees.
Contributed by: D. Meliga, S. Z. Lavagnino and G. Valorio (September 2017)
Additional contributions by: M. Allegretti
Open content licensed under CC BY-NC-SA
Snapshots
Details
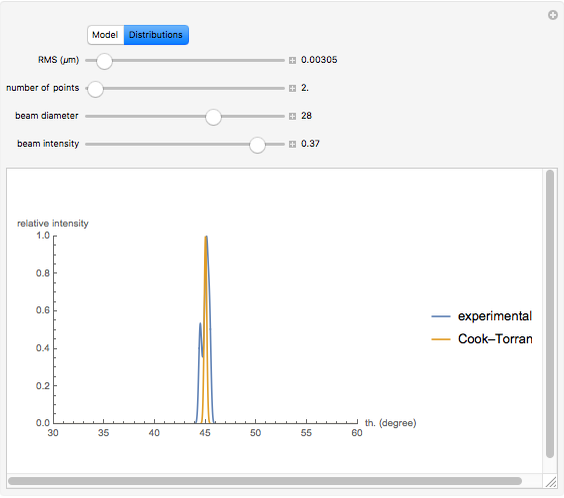
Snapshot 1: in the case of low RMS values, good agreement between the theoretical and experimental models is observed
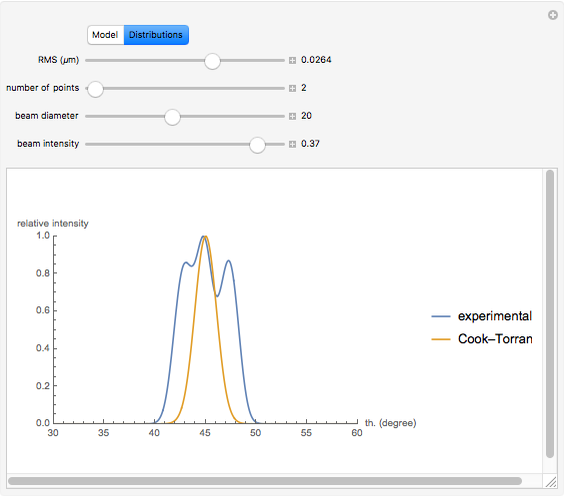
Snapshot 2: in the case of higher RMS values, we begin to detect discrepancy between the theoretical and experimental models
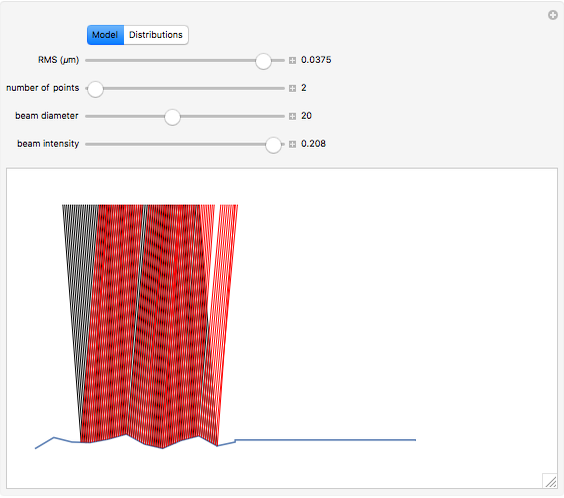
Snapshot 3: a reflection simulation (Snell's law) on a rough surface
References
[1] I. Hajnsek and K. Papathanassiou. "Rough Surface Scattering Models." earth.esa.int/documents/653194/656796/Rough_Surface_Scattering _Models.pdf.
[2] R. L. Cook and K. E. Torrance, "A Reflectance Model for Computer Graphics," ACM Transactions on Graphics, 1(1), 1982 pp. 7–24. doi:10.1145/357290.357293.
Permanent Citation