Comparison of Food Moisture Sorption Isotherm Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
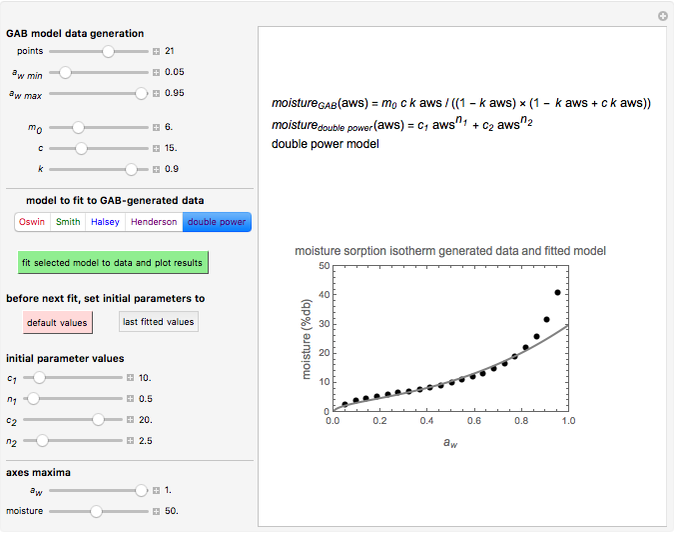
Sigmoid moisture sorption isotherms of foods have been described by a variety of mathematical models having two to four adjustable parameters, the most common of which is the three-parameter GAB model. This Demonstration allows generating moisture sorption isotherm data with this model, based on published parameters values for example, and fitting them with the two-parameter Oswin, Smith, Halsey, or Henderson model, and by the four-parameter double-power model with or without adjusting the water activity range. To facilitate the fit, you can match the generated data by adjusting the chosen model's parameters with sliders prior to executing the nonlinear regression.
Contributed by: Mark D. Normand and Micha Peleg (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
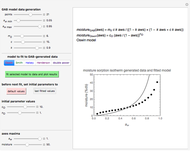
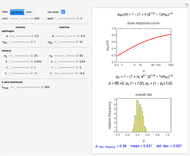
Snapshot 1: sorption isotherm data generated with the three-parameter GAB model and the superimposed two-parameter Oswin isotherm with the default range and initial parameter values
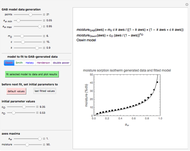
Snapshot 2: sorption isotherm data generated with the three-parameter GAB model and the superimposed two-parameter Oswin isotherm equation with the data range and initial values adjusted
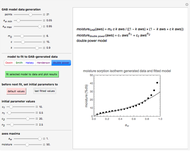
Snapshot 3: sorption isotherm data generated with the three-parameter GAB model and the superimposed four-parameter double-power isotherm equation with the default range and initial parameter values
Snapshot 4: sorption isotherm data generated with the three-parameter GAB model and the superimposed four-parameter double-power isotherm equation with the same data range but initial values adjusted
Snapshot 5: sorption isotherm data generated with the three-parameter GAB model and the superimposed fitted four-parameter double-power isotherm equation
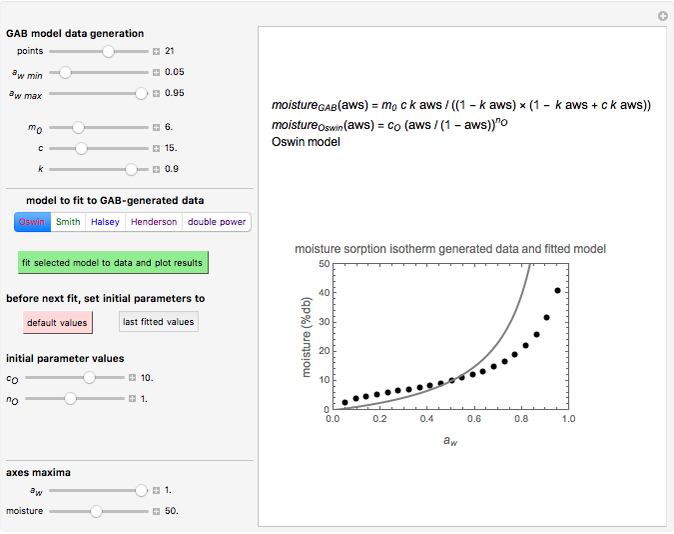
The three-parameter Guggenheim, Anderson, and de Boer (GAB) sorption model is a variant of the more famous two-parameter Brunauer, Emmett, and Teller (BET) model. It has been frequently used to describe sigmoid moisture sorption isotherms and is commonly written in the form 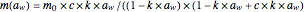 , where
, where 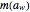 is the equilibrium moisture content in percent on a dry basis (g water/100g dry matter) that corresponds to a water activity level,
is the equilibrium moisture content in percent on a dry basis (g water/100g dry matter) that corresponds to a water activity level, 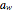 , and
, and 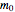 ,
,  , and
, and  are adjustable parameters obtained by curve fitting [1–4]. (The validity of considering
are adjustable parameters obtained by curve fitting [1–4]. (The validity of considering 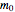 as being the "water monolayer" can be challenged on different grounds, but this should not concern us here.) Alternative models have been the empirical Oswin,
as being the "water monolayer" can be challenged on different grounds, but this should not concern us here.) Alternative models have been the empirical Oswin, 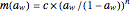 , for
, for  and
and 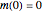 ; Smith,
; Smith, 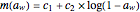 , for
, for 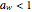 ; Halsey,
; Halsey, 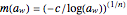 , for
, for  and
and 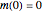 ; Henderson,
; Henderson, 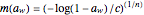 ; and the semi-empirical double-power equation
; and the semi-empirical double-power equation  (also known as the Peleg isotherm), where the
(also known as the Peleg isotherm), where the  's and
's and  's are constants.
's are constants.
Since some of the models cannot be used interchangeably over the entire 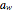 range of 0 to 1, this Demonstration allows fitting the sorption data generated using the GAB parameters with the other five models with or without adjustment of the water activity range, specified by its lower and upper bounds. To facilitate the fit and assure convergence during the regression, you can adjust the gray curve given by the guessed initial parameter values to match the generated data visually. Click the green button "fit selected model to data and plot results" to fit the currently selected model to the generated data using the current slider settings as the initial guesses of the model's parameters. Once the entered initial guesses of the parameters enable a successful fit, the Demonstration will calculate and display the best-fit parameters and will show the fit's correlation coefficient,
range of 0 to 1, this Demonstration allows fitting the sorption data generated using the GAB parameters with the other five models with or without adjustment of the water activity range, specified by its lower and upper bounds. To facilitate the fit and assure convergence during the regression, you can adjust the gray curve given by the guessed initial parameter values to match the generated data visually. Click the green button "fit selected model to data and plot results" to fit the currently selected model to the generated data using the current slider settings as the initial guesses of the model's parameters. Once the entered initial guesses of the parameters enable a successful fit, the Demonstration will calculate and display the best-fit parameters and will show the fit's correlation coefficient, 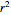 , in blue. It will also superimpose a plot of the fitted curve on the generated data, which is plotted as black dots. The color of the fitted curve matches the color of the text of the currently selected model. If the fit appears to need improvement, you can readjust the initial parameter guesses and repeat the regression until a higher
, in blue. It will also superimpose a plot of the fitted curve on the generated data, which is plotted as black dots. The color of the fitted curve matches the color of the text of the currently selected model. If the fit appears to need improvement, you can readjust the initial parameter guesses and repeat the regression until a higher 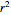 is obtained. "Fit failed!" appears in red if the fit attempt was not successful.
is obtained. "Fit failed!" appears in red if the fit attempt was not successful.
The default appearance of the Thumbnail panel shows 21 data points generated with the GAB model after they have been successfully fitted by the Oswin model. Move any control to erase the displayed fitted parameter and 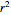 values, replace the red fitted curve with the gray curve representing the current slider-entered parameter values, and activate the green button in preparation for a new fit attempt.
values, replace the red fitted curve with the gray curve representing the current slider-entered parameter values, and activate the green button in preparation for a new fit attempt.
References
[1] H. A. Iglesias and J. Chirife, Handbook of Food Isotherms: Water Sorption Parameters for Food and Food Components, New York: Academic Press, 1982.
[2] W. Wolf, W. E. L. Spiess, and G. Jung, Sorption Isotherms and Water Activity of Food Materials, New York: Elsevier, 1985.
[3] M. Peleg, "Assessment of a Semi-Empirical Four Parameter General Model for Sigmoid Moisture Sorption Isotherms," Journal of Food Process Engineering, 16(1), 1993 pp. 21–37. doi:10.1111/j.1745-4530.1993.tb00160.x.
[4] R. D. Andrade P., R. Lemus M., and C. E. Perez C., "Models of Sorption Isotherms for Food: Uses and Limitations," Vitae, 18(3), 2011 pp. 325–334. aprendeenlinea.udea.edu.co/revistas/index.php/vitae/article/viewFile/10682/9746.
Permanent Citation