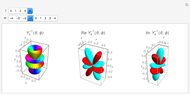
Complex Spherical Harmonics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
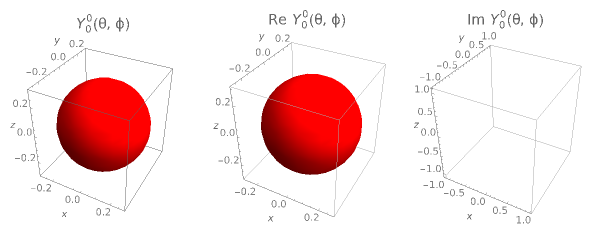
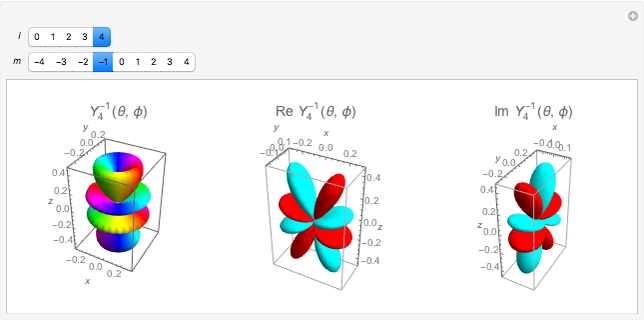
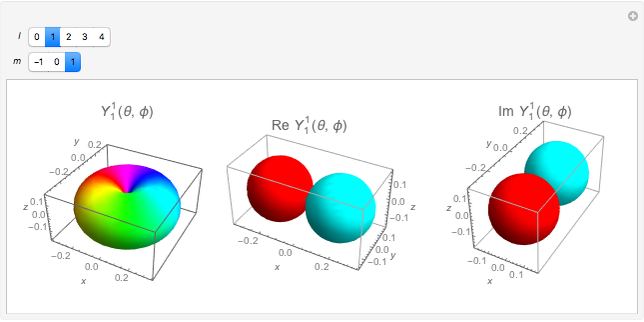
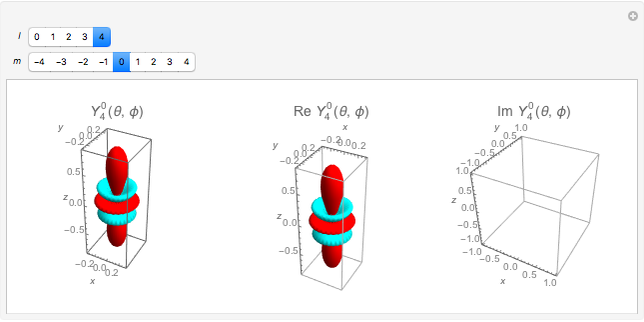
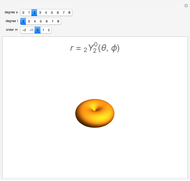
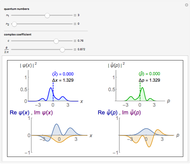
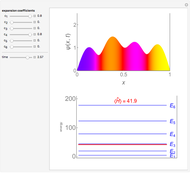
Spherical harmonic functions arise for central force problems in quantum mechanics as the angular part of the Schrödinger equation in spherical polar coordinates. They are given by 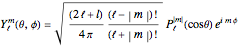 , where
, where 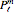 are associated Legendre polynomials and
are associated Legendre polynomials and 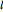 and
and 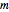 are the orbital and magnetic quantum numbers, respectively. The allowed values of the quantum numbers, which follow from the boundary conditions of the problem, are
are the orbital and magnetic quantum numbers, respectively. The allowed values of the quantum numbers, which follow from the boundary conditions of the problem, are 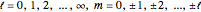 . The complex function
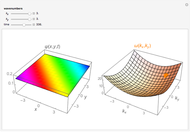
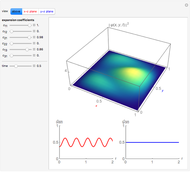
. The complex function  is shown on the left, where the shape is its modulus and the coloring corresponds to its argument, the range 0 to
is shown on the left, where the shape is its modulus and the coloring corresponds to its argument, the range 0 to 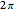 corresponding to colors from red to magenta. The center and right graphics show the corresponding real and imaginary parts.
corresponding to colors from red to magenta. The center and right graphics show the corresponding real and imaginary parts.
Contributed by: Porscha McRobbie and Eitan Geva (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
S. M. Blinder, Introduction to Quantum Mechanics: In Chemistry, Materials Science and Biology, Burlington, MA: Elsevier Academic Press, 2004.
Permanent Citation