Compression Ratio of Spheres in a Curved Tube

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
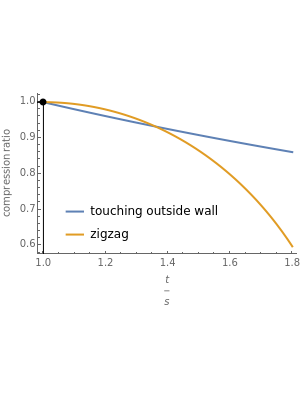
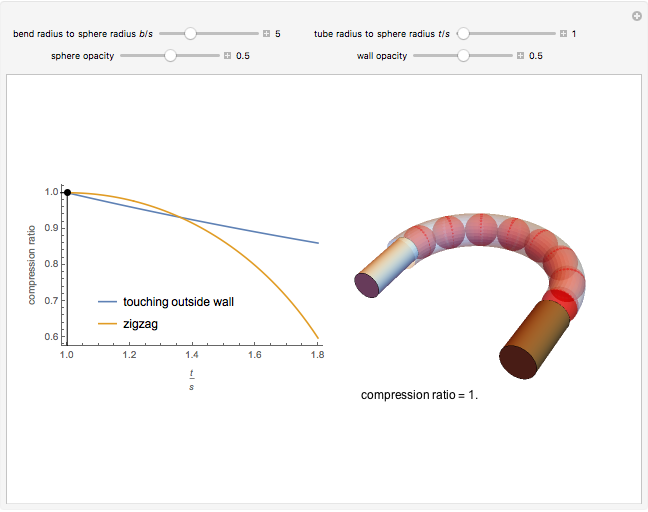
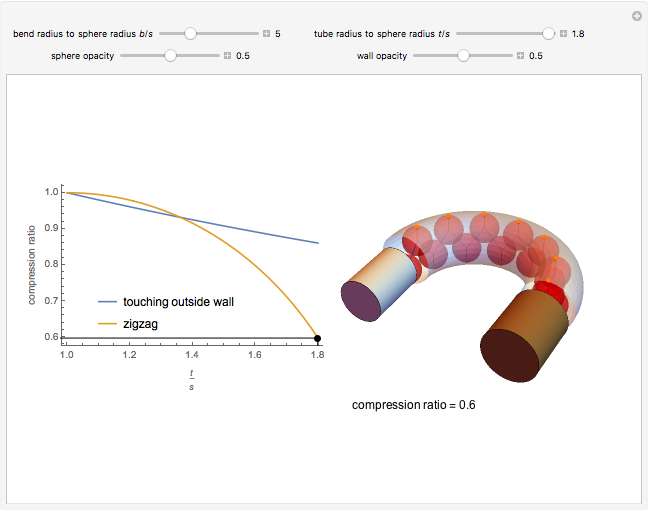
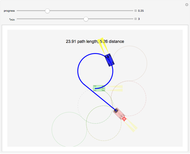
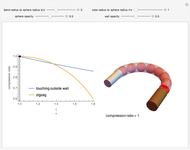
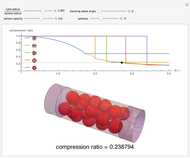
This Demonstration determines the optimal packing for spheres in a curved tube. Spheres of radius  are packed in a tube of radius
are packed in a tube of radius  , where
, where  , with a
, with a 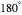 bend of radius
bend of radius  . We seek the minimum value of the compression ratio. For small ratios
. We seek the minimum value of the compression ratio. For small ratios 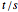 , the spheres are in contact with the outside wall. For larger
, the spheres are in contact with the outside wall. For larger  , optimal compression is attained by arranging the spheres in a zigzag pattern parallel to the axis of curvature along the tube centerline.
, optimal compression is attained by arranging the spheres in a zigzag pattern parallel to the axis of curvature along the tube centerline.
Contributed by: Aaron T. Becker, Haoran Zhao and Li Huang (March 2017)
Open content licensed under CC BY-NC-SA
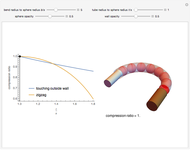
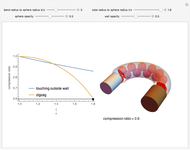
Snapshots
Details
Inside a bend, the spheres arrange themselves so as to minimize the compression ratio; they are all either in contact with the outer wall of the tube or in a zigzag pattern parallel to the axis of curvature along the tube centerline.
If the spheres are centered in the tube, the angular separation between successive spheres is
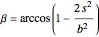 .
.
When the spheres are all flush with the outer wall of the tubing, the angle is
 ,
,
and the compression ratio is
 .
.
For the zigzag pattern, the angle is
 ,
,
and the compression ratio is
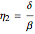 .
.
The transition point occurs when
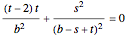 .
.
Permanent Citation