Computation of Radiative Transfer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
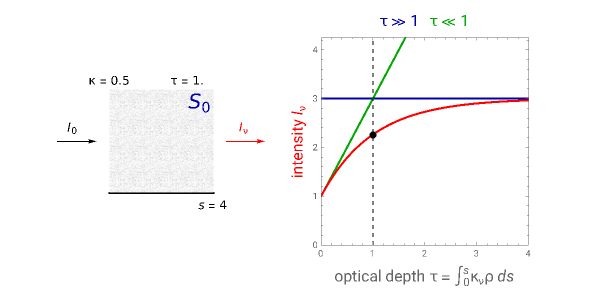
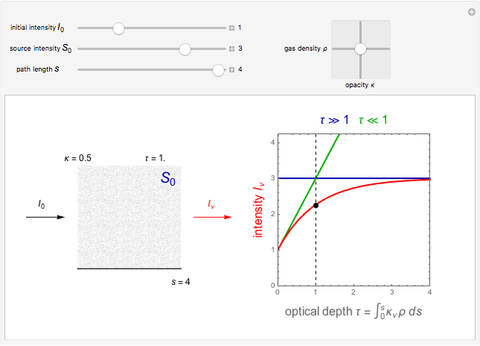
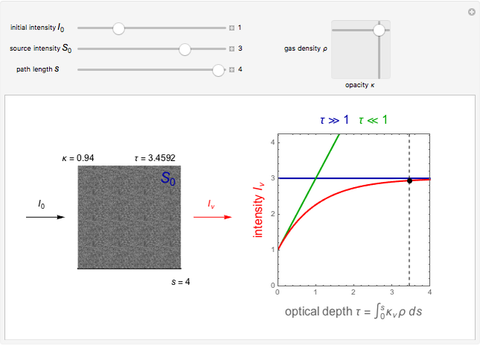
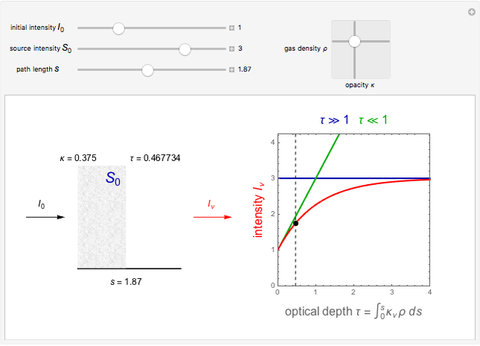
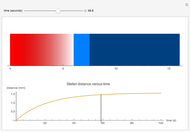
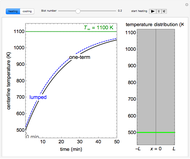
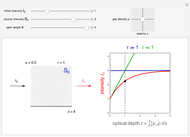
The equation of radiative transfer describes the propagation of radiation and the effects of emission, absorption, and scattering through a medium. This Demonstration shows the simple case of an initial intensity through a volume of gas with no scattering, constant opacity, gas density, and source function intensity. The differential equation is solved and the intensity 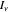 as a result of the radiative transfer through the gas volume is computed as a function of optical depth. The intensity approaches the source function intensity
as a result of the radiative transfer through the gas volume is computed as a function of optical depth. The intensity approaches the source function intensity 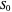 for optically thick cases (
for optically thick cases (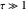 ) and the initial intensity of the background source
) and the initial intensity of the background source 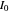 for optically thin cases (
for optically thin cases (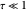 ).
).
Contributed by: Brian Kent (March 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The equation of radiative transfer is given by
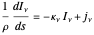 ,
,
where 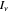 is the specific intensity (red line),
is the specific intensity (red line),  is the gas density,
is the gas density, 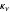 is the opacity or absorption coefficient, and
is the opacity or absorption coefficient, and  is the emission coefficient. The equation describes how incident radiation is affected along a path length
is the emission coefficient. The equation describes how incident radiation is affected along a path length  . We define the source function
. We define the source function  as well as the optical depth
as well as the optical depth 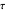 :
:
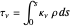
and can rewrite the equation of radiative transfer in terms of 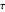 :
:
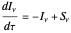 .
.
The formal solution for the specific intensity at a given frequency  for a zero angle of incidence (plane-parallel) is
for a zero angle of incidence (plane-parallel) is
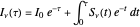 .
.
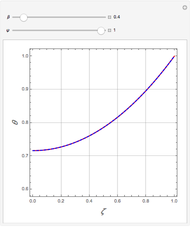
We assume a constant source function 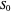 in this Demonstration. The controls let you vary these normalized quantities and show examples where the environment is both optically thin (
in this Demonstration. The controls let you vary these normalized quantities and show examples where the environment is both optically thin (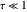 ) and optically thick (
) and optically thick (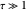 ). The horizontal blue line indicates that for optically thick cases the specific intensity tends toward the constant source function
). The horizontal blue line indicates that for optically thick cases the specific intensity tends toward the constant source function  . For optically thin cases, the specific intensity can be approximated by the green line as
. For optically thin cases, the specific intensity can be approximated by the green line as
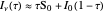 .
.
In-depth studies of these relations can be found in [1] and [2].
References
[1] B. W. Carroll and D. A. Ostlie, An Introduction to Modern Astrophysics, New York: Addison–Wesley, 1996.
[2] G. B. Rybicki and A. P. Lightman, Radiative Processes in Astrophysics, New York: Wiley–Interscience, 1979.
Permanent Citation