Concentration Profiles in Electrochemical Impedance Spectroscopy (EIS)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
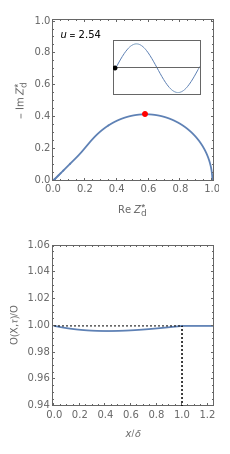
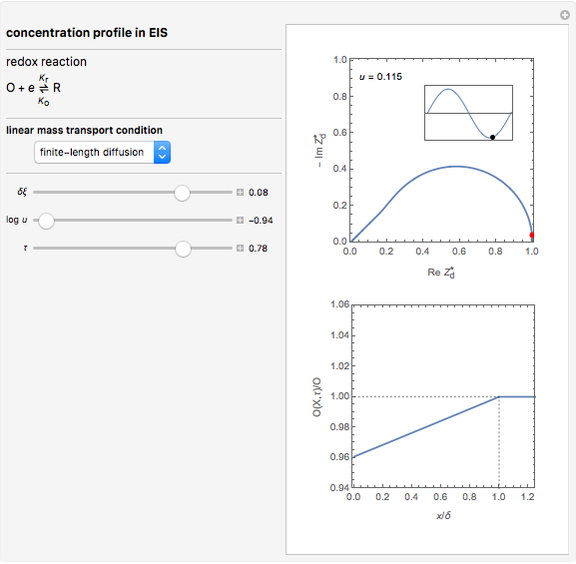
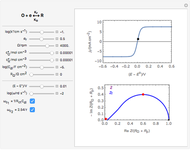
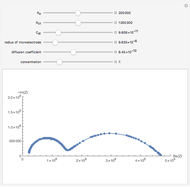
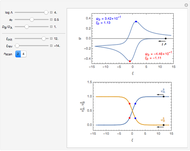
This Demonstration models the time dependence of the concentration profile for the soluble species  involved in a reversible electron transfer reaction
involved in a reversible electron transfer reaction  , taking place at the surface of a planar macroelectrode. The electrode potential is treated as a sinusoidal perturbation. The model assumes finite diffusion in the electrolyte, with a permeable or impermeable boundary condition at the distance
, taking place at the surface of a planar macroelectrode. The electrode potential is treated as a sinusoidal perturbation. The model assumes finite diffusion in the electrolyte, with a permeable or impermeable boundary condition at the distance  from the electrode surface (the so-called finite-length diffusion or restricted diffusion), respectively. You can experiment with the effects of the amplitude of sinusoidal perturbation, the decimal logarithm of its frequency and the time variable, using the controls for the dimensionless parameters
from the electrode surface (the so-called finite-length diffusion or restricted diffusion), respectively. You can experiment with the effects of the amplitude of sinusoidal perturbation, the decimal logarithm of its frequency and the time variable, using the controls for the dimensionless parameters 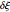 ,
, 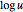 and
and  , respectively.
, respectively.
Contributed by: Claude Montella and Jean-Paul Diard (March 2017)
Univ. Grenoble Alpes, LEPMI, Grenoble, France
Open content licensed under CC BY-NC-SA
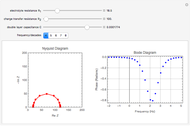
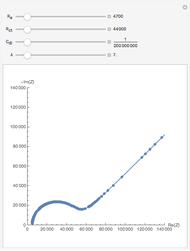
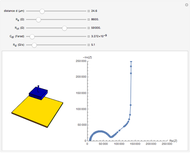
Snapshots
Details
This Demonstration shows on the dimensionless concentration profile for the species  involved in the electron transfer reaction
involved in the electron transfer reaction  . The perturbation signal is a sinusoidal variation of the electrode potential. Two mass transport conditions in the electrolyte are taken into account: (1) finite-length diffusion with constant concentrations of redox species at the distance
. The perturbation signal is a sinusoidal variation of the electrode potential. Two mass transport conditions in the electrolyte are taken into account: (1) finite-length diffusion with constant concentrations of redox species at the distance  from the electrode/electrolyte interface; and (2) restricted diffusion with an impermeable boundary condition (zero flux) at the distance
from the electrode/electrolyte interface; and (2) restricted diffusion with an impermeable boundary condition (zero flux) at the distance  from the interface.
from the interface.
The model assumes that:
(i) the electrode is uniformly accessible,
(ii) the electrochemical reaction has reversible kinetics,
(iii) the double-layer charging current is neglected,
(iv) the faradaic impedance is calculated at the equilibrium potential of the electrode and
(v) both redox species  and
and  have the same initial concentrations and same diffusion coefficients.
have the same initial concentrations and same diffusion coefficients.
Dimensionless quantities are defined for all variables/parameters; that is, the distance from the interface 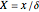 , the time variable
, the time variable  , the interfacial concentration
, the interfacial concentration  , the angular frequency of sinusoidal signal
, the angular frequency of sinusoidal signal 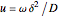 , its amplitude
, its amplitude  and the diffusion impedance
and the diffusion impedance 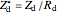 . Here
. Here  denotes the initial concentration,
denotes the initial concentration,  is the diffusion coefficient,
is the diffusion coefficient, 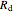 is the diffusion resistance and
is the diffusion resistance and  is the Nernst constant, with
is the Nernst constant, with  ,
, 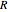 and
and  having their usual meanings.
having their usual meanings.
Of course, semi-infinite diffusion conditions can be recovered at high frequencies, typically at  , irrespective of the permeable or impermeable boundary at
, irrespective of the permeable or impermeable boundary at  .
.
General rules for computing the species concentration versus distance and time are given in [1].
Reference
[1] C. Montella, J.-P. Diard and B. Le Gorrec, Exercices de cinétique électrochimique : II. Méthode d’impédance, Paris: Éditions Hermann, 2005 pp. 237.
Permanent Citation