Concurrent and Countercurrent Cooling in Tubular Reactors with Exothermic Chemical Reactions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
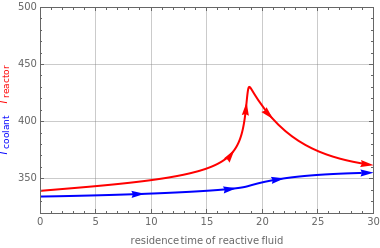
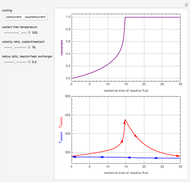
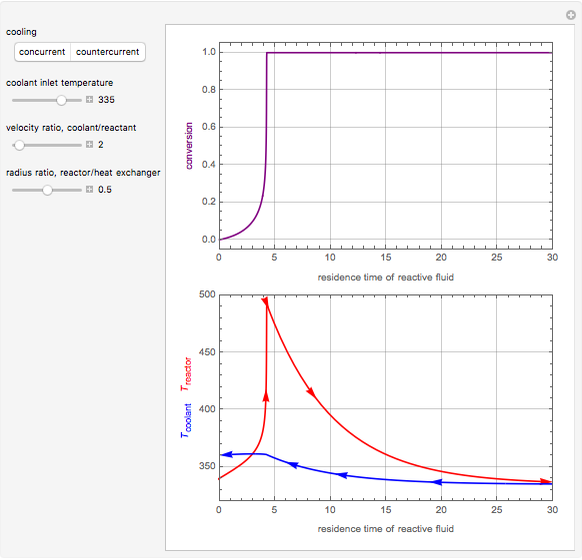
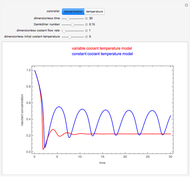
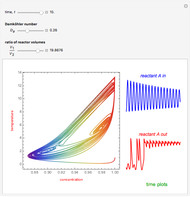
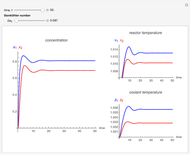
The object of this Demonstration is to observe thermal runaway in a tubular reactor and identify the critical parameters that represent the crossover from a thermally well-behaved reactor to one that exhibits thermal runaway.
[more]
Contributed by: Clay Gruesbeck (March 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Mass balance for reactant 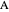 :
:
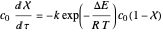 ,
,
where 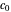 is the initial concentration of
is the initial concentration of 
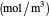 ,
, 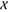 is the dimensionless variable,
is the dimensionless variable, 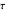 (s) is the residence time of the reactive fluid,
(s) is the residence time of the reactive fluid,  stands for the pre-exponential rate factor
stands for the pre-exponential rate factor 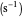 ,
,  is the activation energy
is the activation energy 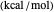 ,
,  is the gas constant
is the gas constant 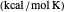 , and
, and  is the temperature of the reactants
is the temperature of the reactants 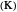 .
.
Thermal balance for reactive fluid within the inner pipe:
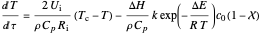 ,
,
where  is the average reactants density
is the average reactants density 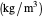 ,
,  is the heat capacity
is the heat capacity 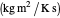 ,
, 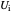 is the inner pipe overall heat transfer coefficient
is the inner pipe overall heat transfer coefficient 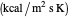 ,
, 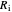 is the radius for the inner pipe
is the radius for the inner pipe  ,
, 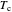 is the coolant temperature
is the coolant temperature 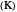 , and
, and 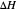 is the heat of reaction
is the heat of reaction 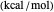 .
.
Thermal balance for concurrent cooling fluid in the annulus:
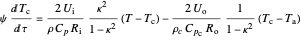 .
.
The equation for countercurrent cooling differs from the above equation by a negative sign because integration is opposite to the direction of flow. Here 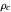 is the coolant density
is the coolant density 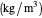 ,
, 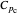 is the coolant heat capacity
is the coolant heat capacity  ,
,  is the ratio of the velocity of the coolant to reactant fluid,
is the ratio of the velocity of the coolant to reactant fluid, 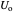 is the outer pipe overall heat transfer coefficient
is the outer pipe overall heat transfer coefficient 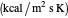 ,
, 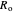 is the radius of the outer pipe
is the radius of the outer pipe 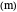 ,
,  is the ratio
is the ratio 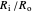 , and
, and 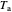 is the ambient temperature
is the ambient temperature  .
.
This split boundary value problem is solved with:
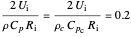 ,
, 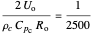 .
.
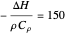 ,
, 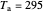 ,
, 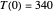 ,
, 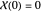 ,
, 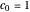 ,
, 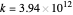 and
and 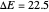 ,
,
with user-selected direction of coolant and values of  ,
,  and
and  .
.
Reference
[1] L. A. Belfiore, Transport Phenomena for Chemical Reactor Design, Hoboken, NJ: John Wiley & Sons, 2003.
Permanent Citation