Conditionally Reversible Elementary Cellular Automata

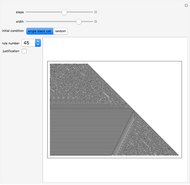
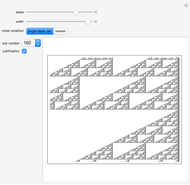
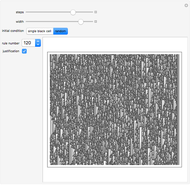
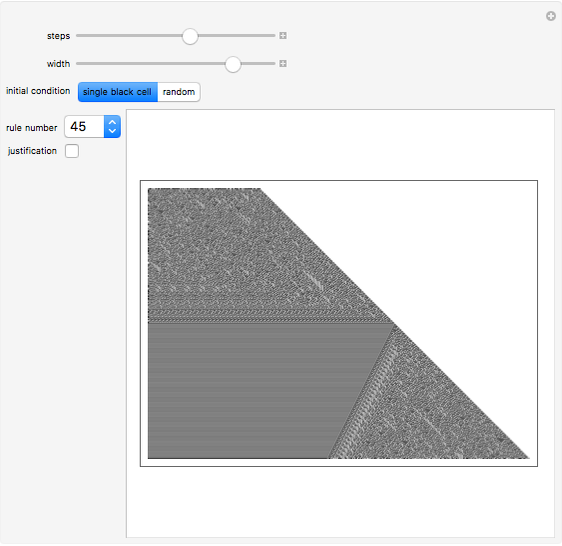
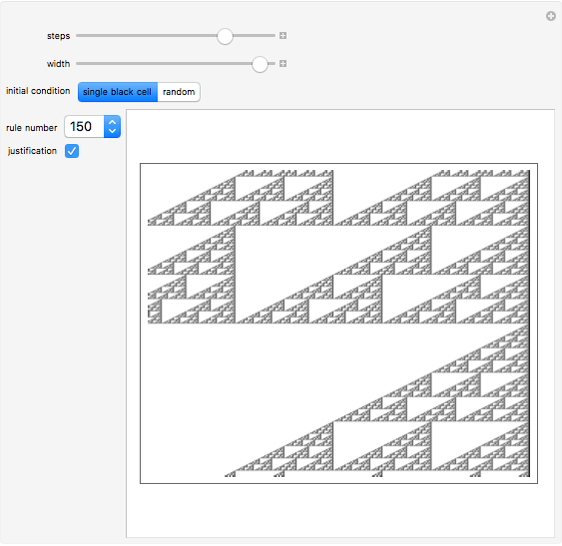
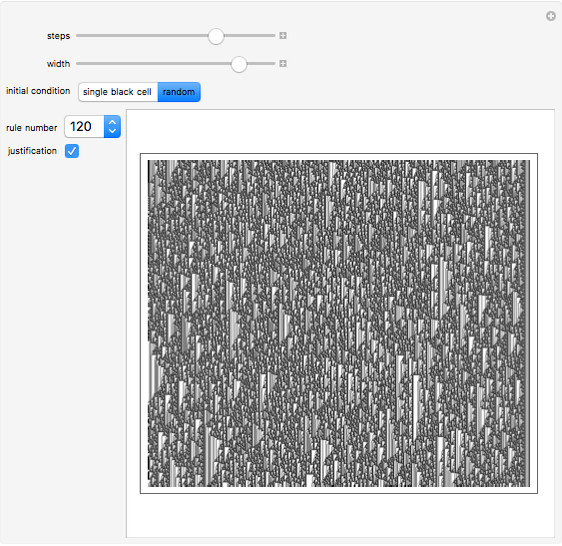
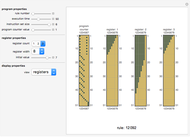
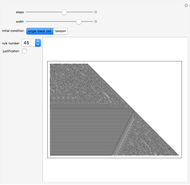
Of the 256 elementary cellular automata, 16 have the property that changing the left bit in the rule icon always changes the output bit. These rules are called left bijective or said to exhibit one-sided additivity, and they can be run uniquely backward in time from initial conditions with certain background colors. This Demonstration explores the 12 of these 16 rules that support unique histories from a white background. See what the history looks like from a single black cell or from a random initial condition.