Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Cone Geodesics

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

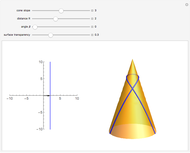
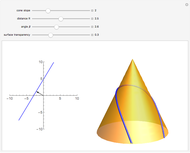
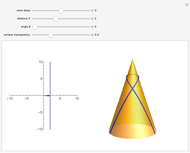
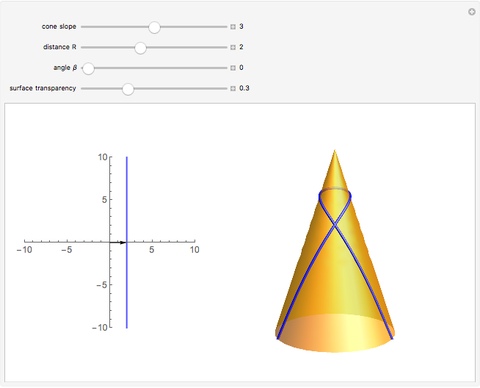
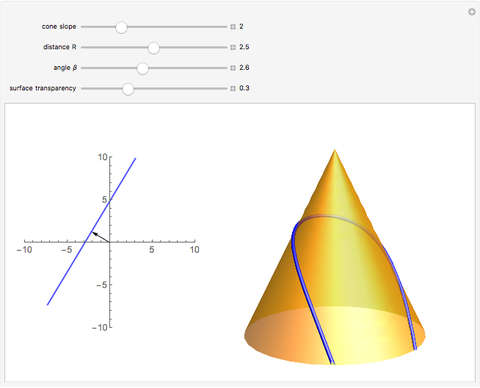
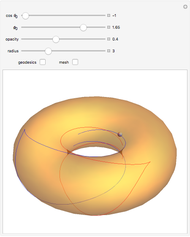
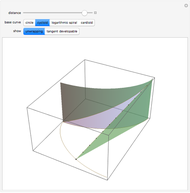
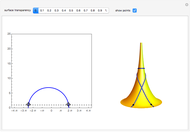
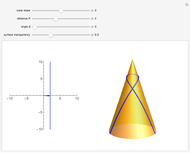
Geodesics on a cone are easily found using the fact that the surface is isometric to the plane. The left image shows a line specified by two parameters,  (distance from the origin) and  (angle between the normal vector and the horizontal axis). The right part shows a cone together with the geodesic that represents an isometric image of the given line.

Contributed by: Antonin Slavik (March 2011)
Charles University, Prague
Open content licensed under CC BY-NC-SA

Snapshots

Details

Assuming that the plane is parametrized using polar coordinates as and the cone as , the isometry between the two surfaces is given by , .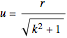

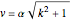In rectangular coordinates, the line in the plane is parametrized as , . These coordinates have to be transformed to polar coordinates before applying the isometry.

Making the surface semitransparent gives a better overview of the geodesic behavior, but decreases the visualization performance.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send