Confidence Interval Exploration

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
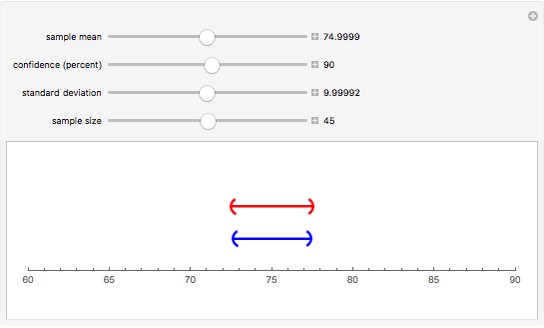
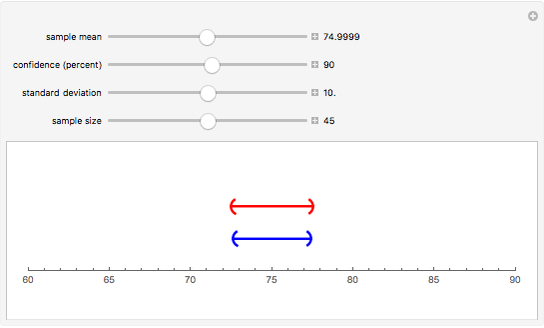
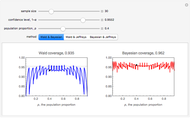
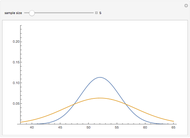
Use the sliders to change the various quantities that go into determining the confidence interval for the population mean and see how the upper (red) interval is affected. The lower (blue) interval was found using the default starting values and remains unchanged for comparison purposes. The intervals are approximate, and for small samples require some normality in the underlying population to be good approximations.
Contributed by: David Gurney (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Formulas for the confidence interval for the population mean can be found in most elementary statistics texts. In the case when the population standard deviation is known, the confidence interval formula is given in A. G. Bluman, Elementary Statistics, 6th ed., New York: McGraw–Hill, 2007 p. 351.
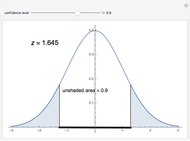
Instead of using a single number as an estimate for the population mean, statisticians use interval estimates because the interval's probability of containing the population mean is much higher than a single number's probability of matching the population mean. Roughly speaking, the probability that an interval contains the population mean is called the confidence level. Confidence levels usually range from 80% to just below 100%.
Without data from the entire population, which is the usual case, statisticians cannot be 100% certain that an interval will contain the population mean. If the confidence level is increased, the interval must be larger and there is less information about where the population mean might be; but if the interval is made smaller, there is less chance that the interval contains the population mean. This type of trade-off happens a lot in statistics.
Permanent Citation
"Confidence Interval Exploration"
http://demonstrations.wolfram.com/ConfidenceIntervalExploration/
Wolfram Demonstrations Project
Published: March 7 2011