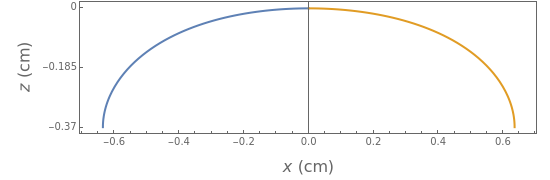
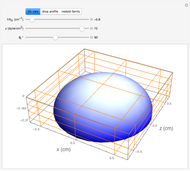
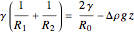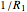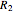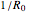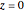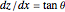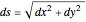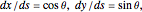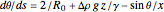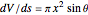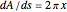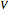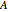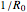Configuration of a Sessile Drop

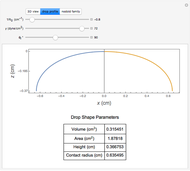
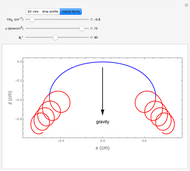
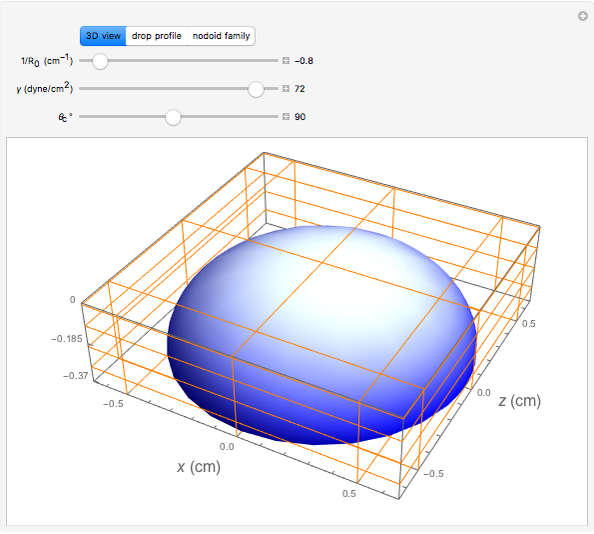
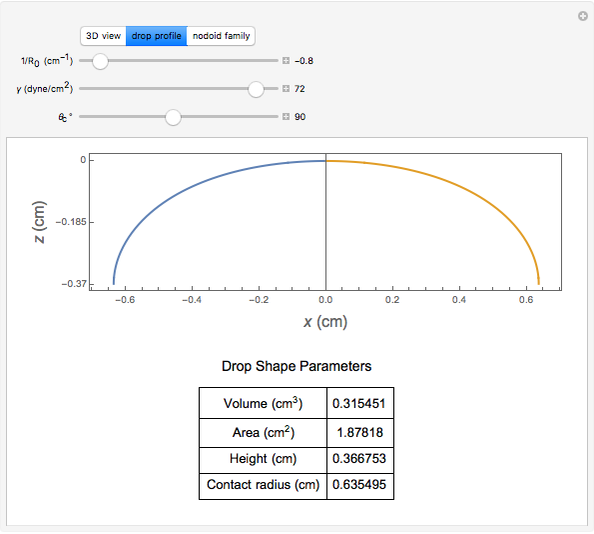
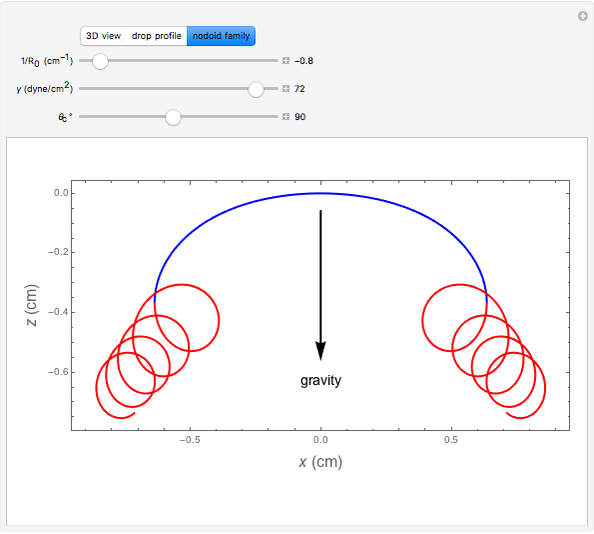
When a drop of liquid with interfacial tension is placed on a non-wetting solid surface, the drop assumes a shape that is determined by the contact angle 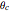that the liquid makes at the three-phase contact line, in accordance with the Young–Dupré equation (see [1]). Under static conditions, the drop shape must also satisfy the Young–Laplace equation of capillarity, which describes the mechanical equilibrium for two homogeneous fluids separated by an interface:

,

where and 1/ are the two principal curvatures of the drop and is a reference curvature at the drop apex ().

In this Demonstration the shape of an axisymmetric sessile drop is computed for given , , and contact angle . The liquid is taken to be water and the surrounding fluid is air. For computational purposes it is convenient to work with arc length along the curve and the turning angle , which is defined in terms of the local slope by . Introducing and the arc length (i.e., ) as new variables along the interface allows the Young–Laplace equation to be expressed as

and , , ,

where is the volume and the surface area of the drop. Thus for a given and , specifying the reference curvature is equivalent to specifying the volume or surface area of the drop. (or ) decreases monotonically with increasing .

The sliders let you investigate how the shape of the drop depends on the surface tension (to simulate the effect of temperature or the presence of a surfactant), the contact angle , and the radius of curvature at the drop apex. Either the shape of the drop (a 3D rendition, or its cross sectional profile) can be selected. The button "family of nodoids" displays the nodoid shape family from which the sessile drop belongs (see the blue portion of the curve). The characteristic feature of the nodoid family is that it does not have an inflection point.