Conformal Mapping of the Unit Disk

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
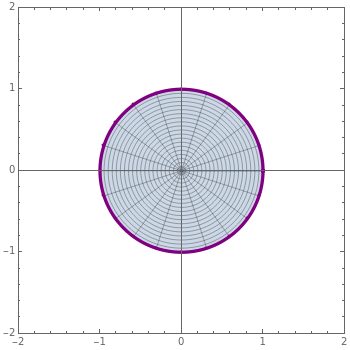
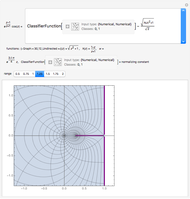
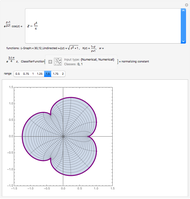
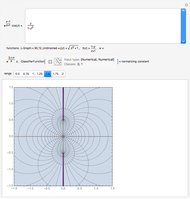
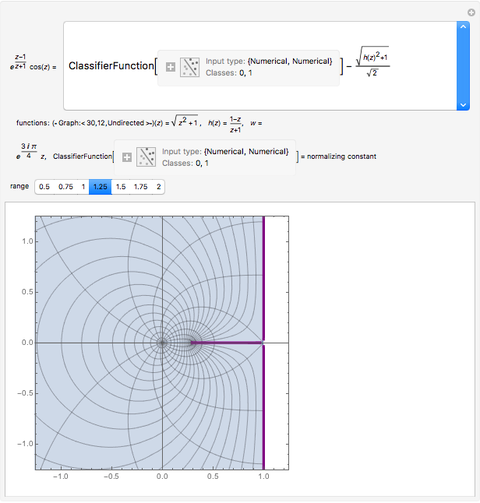
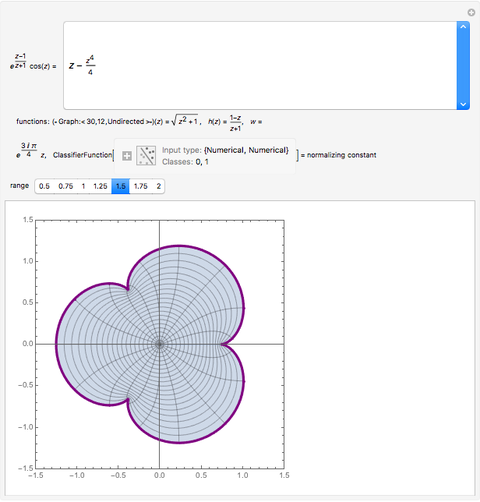
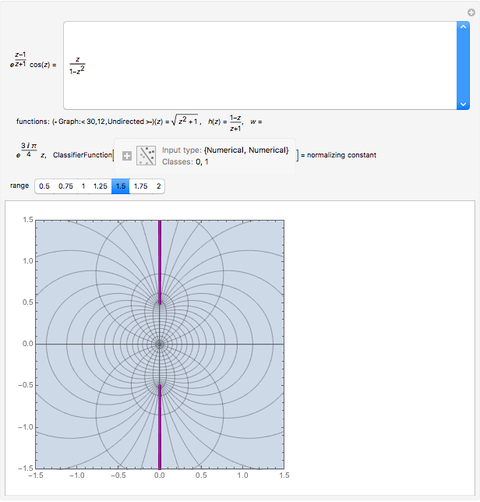
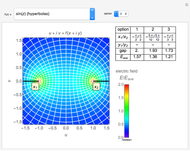
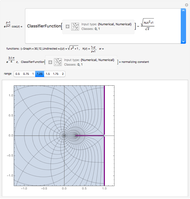
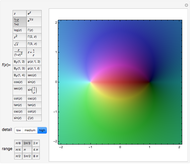
The famous Riemann mapping theorem states that any simply connected domain in the complex plane (other than the whole plane itself) is conformally equivalent to the unit disk. However, finding an explicit conformal map for a given domain can be a tedious task. This Demonstration plots the image of the unit disk under various conformal maps 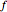 , normalized so that
, normalized so that 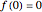 and
and  . Each plot shows the images of concentric circles around the origin and radial lines emanating from the origin.
. Each plot shows the images of concentric circles around the origin and radial lines emanating from the origin.
Contributed by: Matthew Romney (March 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Conformal mapping is a bijective, angle-preserving function between two domains in the complex plane. A standard result of complex analysis states that every injective analytic function of a complex variable is a conformal mapping onto its image, and conversely that every conformal mapping is an analytic function of a complex variable.
By the Riemann mapping theorem, every simply connected proper subdomain of the complex plane is conformally equivalent to the unit disk. The study of conformal mappings on the unit disk led to a classical branch of mathematics called univalent functions, which was pursued for most of the twentieth century. This Demonstration plots a number of conformal maps defined on the unit disk, each one normalized (as is customary in this subject) so that 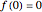 and
and  . Each plot shows the images of concentric circles around the origin and radial lines emanating from the origin.
. Each plot shows the images of concentric circles around the origin and radial lines emanating from the origin.
Many of the functions here can be derived using Schwarz–Christoffel integrals. A few are based on examples from [2].
References
[1] E. B. Saff and A. D. Snider, Fundamentals of Complex Analysis with Applications to Engineering, Science, and Mathematics, 3rd ed., Upper Saddle River: Prentice Hall, 2003.
[2] J. H. Matthews and R. W. Howell, "Dictionary of Confomal Mapping." (Mar 18, 2016) mathfaculty.fullerton.edu/mathews/c2003/ConformalMapDictionary.1.html.
Permanent Citation