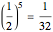Consecutive Heads or Tails

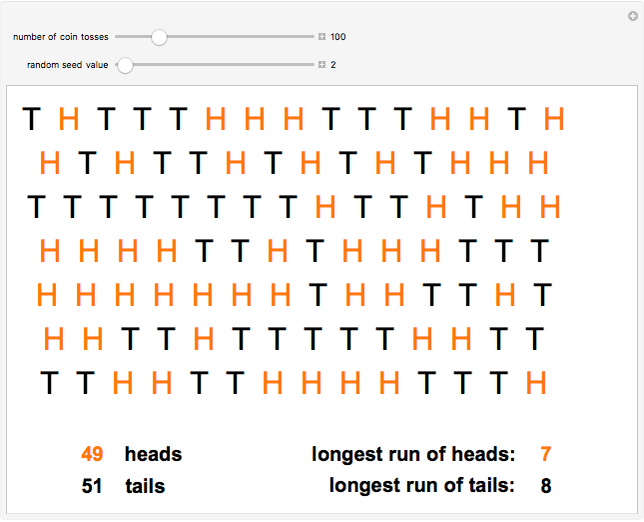
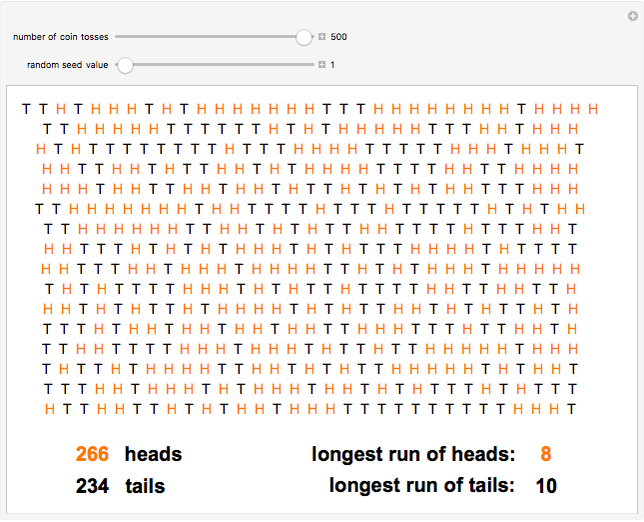
For a homework assignment in a statistics course, half the class was asked to record the actual results of 100 coin tosses while the other half was asked to fake the same results by writing down what they thought might be a reasonable random sequence of heads and tails. With only a quick glance at a student's homework, the professor was able to determine whether the statistics were real or faked, with 90% accuracy! The giveaway clue was the occurrence of runs of 5, 6 or even 7 consecutive heads or tails. These are likely to occur in actual sequences, contrary to some naive intuitive notions about randomness.

This feature of random distributions is fairly simple to deduce. Since the probability of heads in a single coin toss is , the probability of a run of five heads equals . But a series of 100 coin tosses contains 96 sequences of length five. So there is a strong likelihood that at least one run of five heads (or tails) will occur; in fact, an 81% chance. Analogously, runs of 6 occur with a probability of 55%, runs of 7 with 32% and runs of 8 with 16%.

In this Demonstration, Mathematica's random number generator simulates up to 500 coin tosses. You can generate a new sequence of heads and tails by changing the seed value.

Similarly, every basketball player is likely to experience both "hot" and "cold" shooting streaks, like the runs of heads or tails shown here. This is an unavoidable consequence of the mathematics of statistics. However, many players and coaches refuse to believe this!