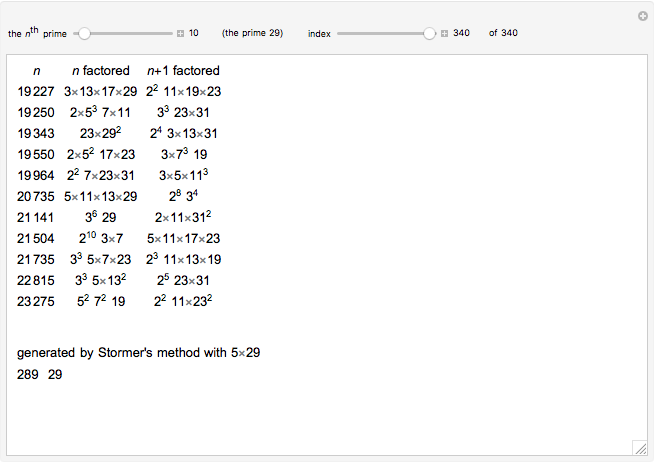
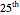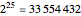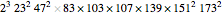Consecutive Smooth Numbers

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The smoothness of a number is its maximal prime factor. The number 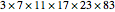 has smoothness 83,
has smoothness 83,  has smoothness 37, and
has smoothness 37, and  has smoothness 97. All three numbers can be considered to be 97-smooth as well, since
has smoothness 97. All three numbers can be considered to be 97-smooth as well, since  and
and  . Multiplied out, these numbers are 7496643, 7496644, and 7496645, making this a consecutive 97-smooth triplet.
. Multiplied out, these numbers are 7496643, 7496644, and 7496645, making this a consecutive 97-smooth triplet.
Contributed by: Ed Pegg Jr (March 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] Wikipedia. "Størmer's Theorem." (Mar 10, 2016) en.wikipedia.org/wiki/St% C3 % B8rmer's_theorem.
[2] D. Eppstein, "Smooth Pairs," LiveJournal (blog). (Mar 23, 2007) 11011110.livejournal.com/97325.html?thread=351533.
Permanent Citation