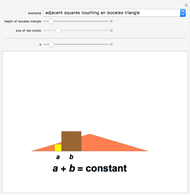
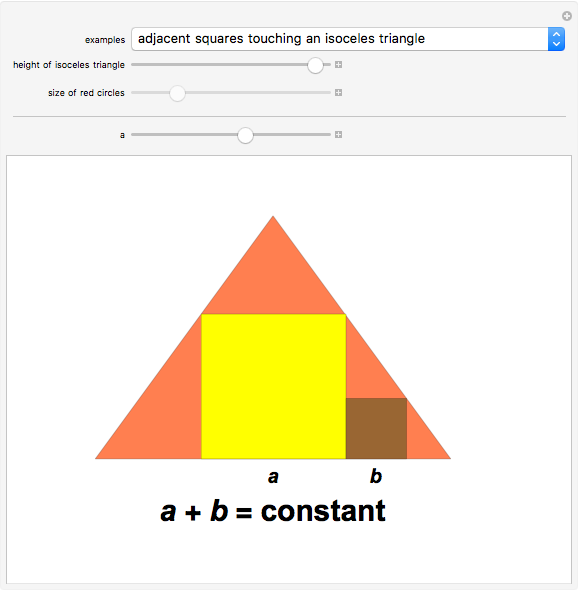
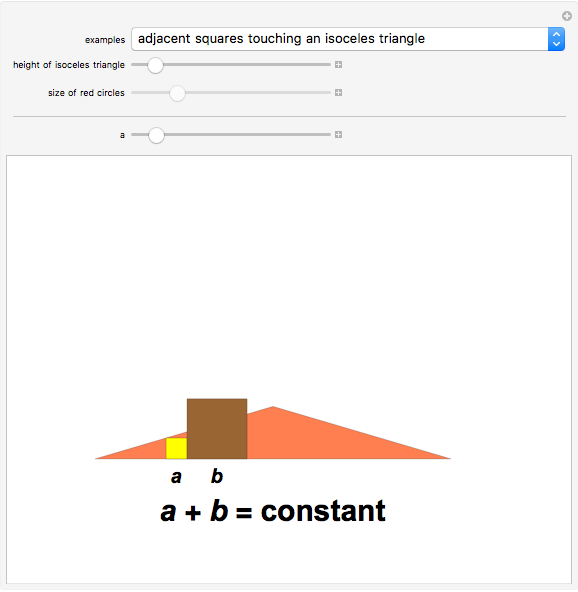
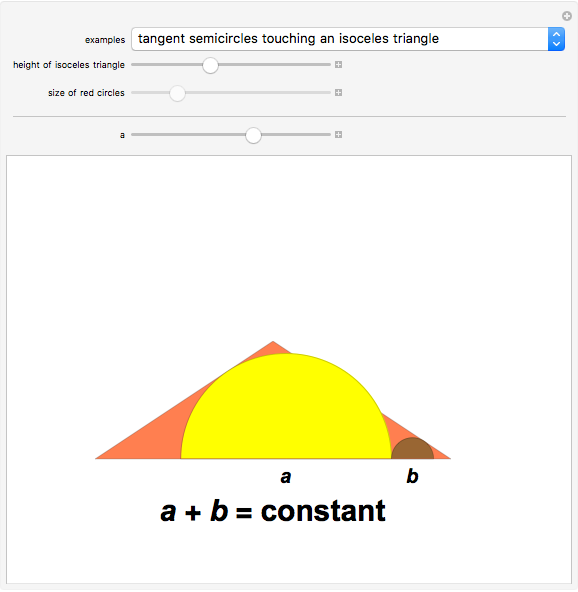
Constant-Sum Figures
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
This Demonstration shows four examples of interesting figures in which a quantity that depends on two others that vary stays constant as long as some geometric condition is met. The two variables are the lengths of the sides  and
and  of two squares or the diameters of two circles.
of two squares or the diameters of two circles.
Contributed by: Jaime Rangel-Mondragon (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] L. C. Tien, "Constant-Sum Figures," The Mathematical Intelligencer, 23(2), 2001 pp. 15–16.
Permanent Citation