Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Contracting the Double-Twist in SO(3)

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

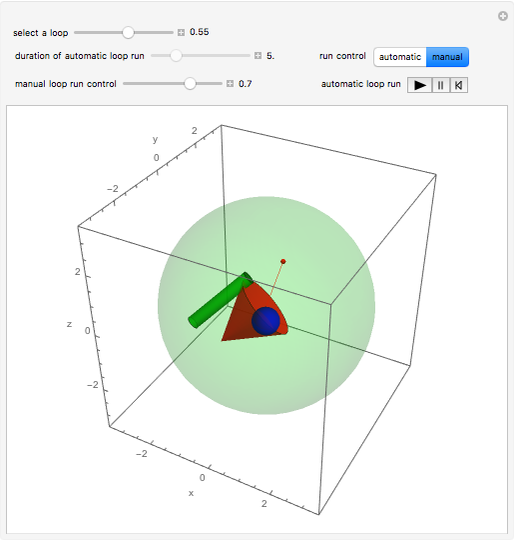
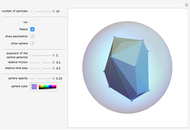
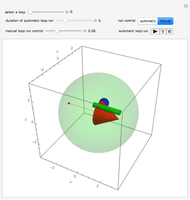
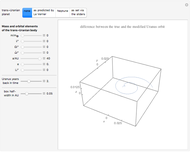
As shown by Dirac's famous belt trick, a double-twist, when viewed as a closed path in the rotation group 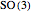, can be continuously contracted to a point. This Demonstration makes the same argument by a more conventional visualization in terms of a moving body, here an asymmetric assembly of a cone, a sphere, and a cylinder. All its motions leave a certain body-fixed point invariant and thus, the attitudes (as in "attitude control in satellites") of the body are in one-to-one correspondence with the elements of 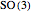, if a reference attitude is agreed upon. Here, the reference attitude is shown if the first slider shows the value 1. Any position of the first slider determines a "loop run", which is a jerk-free motion starting and ending with the reference attitude.

[more]

Together with the attitude of the body, the corresponding element of is shown as a red line ending in a small red sphere. The direction of the line shows the rotation axis and its length the rotation angle. Rotation angles equal to correspond to the surface of a sphere, which is shown here as nearly transparent. It is important to notice that antipodal points on the surface correspond to the same group element, so that jumping from one point to its antipode is no sign of discontinuity of motion.

This Demonstration should convince you that a full swing of the first slider changes the loops that correspond to the various slider positions in a jerk-free manner from a double twist through a phase of more complex motion into a damped oscillation and finally to total rest.

To put this into perspective, notice that a corresponding transformation is not possible for the single-twist.

[less]

Contributed by: Ulrich Mutze (May 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

The paths here are polygons in the - 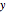plane and are straightforward to program. For a more aesthetic motion, one would have to smooth the kinks and could allow the rotation axis leave the - 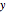plane. To keep the program small, I used a few graphical primitives for the turning object. My first experiments were with a tripod of mutually orthogonal red, green, and blue arrows. This made it much more difficult to memorize complex motion patterns than it is with the present sphere-cone-cylinder assembly.

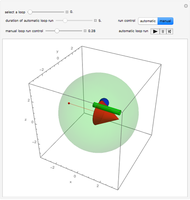
Snapshot 1: a bit more than a quarter of the initial double-twist is done

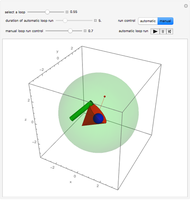
Snapshot 2: complex motion phase

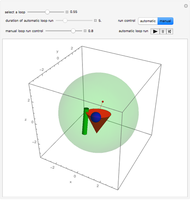
Snapshot 3: complex motion phase, a bit later in the same loop

Snapshot 4: in the final oscillation phase

Snapshot 5: in the final position, the reference position

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send