Convergence of Newton's Method for Approximating Square Roots

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
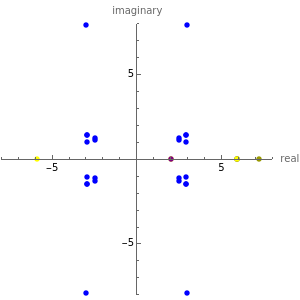
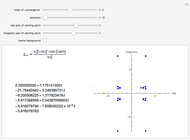
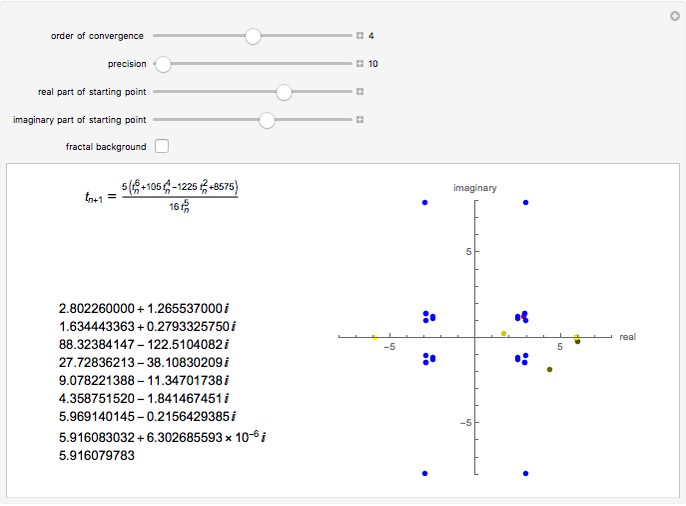
This Demonstration shows the convergence properties of a family of Newton-like methods for computing square roots of positive reals as constructed by Hernández and Romero. In this Demonstration the roots of 35 are used. For each integer  , the iterative formula (displayed in the top left‐hand corner) is defined. It generates a sequence (displayed below the formula) converging to one of the roots of 35 for almost all chosen starting values in the complex plane, outside the imaginary axis. The initial point is shown in purple, the two roots (limit points) are colored yellow, and some of the intermediate points are colored in shades of yellow, with darker colors corresponding to later positions in the sequence.
, the iterative formula (displayed in the top left‐hand corner) is defined. It generates a sequence (displayed below the formula) converging to one of the roots of 35 for almost all chosen starting values in the complex plane, outside the imaginary axis. The initial point is shown in purple, the two roots (limit points) are colored yellow, and some of the intermediate points are colored in shades of yellow, with darker colors corresponding to later positions in the sequence.
Contributed by: Andrzej Kozlowski (March 2011)
After work by: M. A. Hernández and N. Romero
Open content licensed under CC BY-NC-SA
Snapshots
Details
The well-known classical iterative method for computing the square root of a positive real number is globally convergent in the entire complex plane with the imaginary axis removed: initial points in the half‐plane  produce sequences convergent to the positive square root, while those in the half-plane
produce sequences convergent to the positive square root, while those in the half-plane 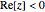 converge to the negative square root. Hernández and Romero constructed for each
converge to the negative square root. Hernández and Romero constructed for each 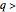 2 an iterative method that exhibits a much more complicated behavior. For each
2 an iterative method that exhibits a much more complicated behavior. For each 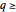 2 these sequences have convergence order
2 these sequences have convergence order  (so for "generic initial" points larger
(so for "generic initial" points larger  should produce a shorter sequence). For even
should produce a shorter sequence). For even  these methods have the property of "global convergence" on the real line, that is, they converge to one of the roots starting with any nonzero value on the real line. For odd
these methods have the property of "global convergence" on the real line, that is, they converge to one of the roots starting with any nonzero value on the real line. For odd  the methods have the property of "general convergence" (a concept introduced by Smale)—that is, they converge for almost every starting point. In the complex plane the behavior of convergence with respect to different starting points is highly complex and displays an intricate fractal structure. Some points of the Julia set of this structure are displayed in blue. In particular, for odd
the methods have the property of "general convergence" (a concept introduced by Smale)—that is, they converge for almost every starting point. In the complex plane the behavior of convergence with respect to different starting points is highly complex and displays an intricate fractal structure. Some points of the Julia set of this structure are displayed in blue. In particular, for odd  there are always points in the Julia set lying on the real line (these are the fixed points of the iteration).
there are always points in the Julia set lying on the real line (these are the fixed points of the iteration).
Checking the checkbox "fractal background" will show initial points that give rise to sequences converging to the positive square root (red) and those that give rise to sequences converging to the negative square root (green). (Unfortunately, to see the fractal nature of the convergence phenomenon we need a much larger number of points, which would excessively slow down the Demonstration).
Reference: M. A. Hernández and N. Romero, "Methods with Prefixed Order for Approximating Square Roots with Global and General Convergence," Applied Mathematics and Computation, 194(2), 2007 pp. 346–353.
Permanent Citation