Correlated Lévy Processes via Lévy Copulas

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
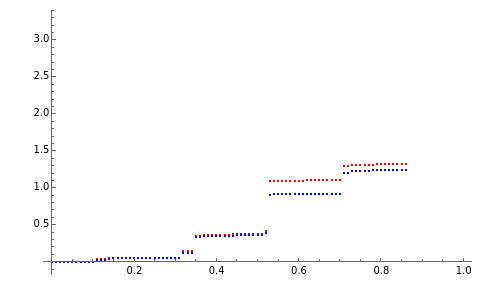
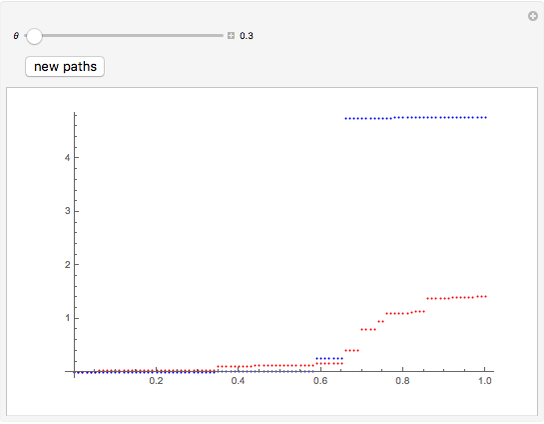
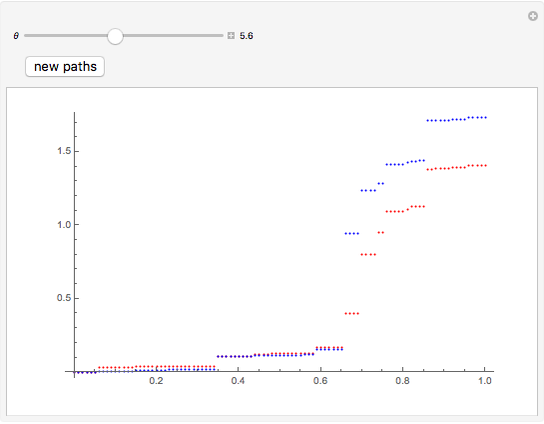
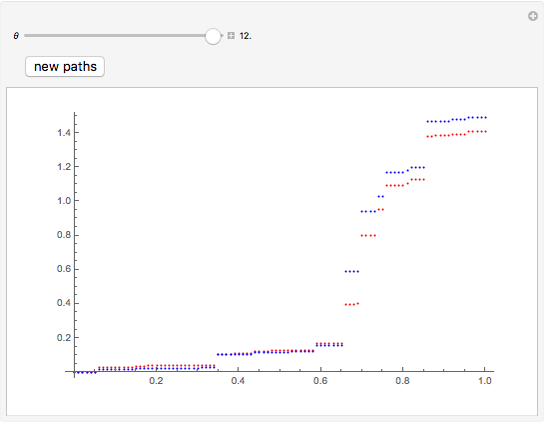
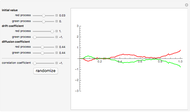
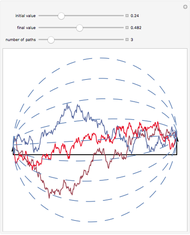
This Demonstration shows a path of a two-dimensional subordinator (Lévy process with only positive jumps) whose components are  -stable Lévy processes with dependence structure given by the Clayton–Lévy copula with parameter
-stable Lévy processes with dependence structure given by the Clayton–Lévy copula with parameter  , which determines the degree of dependence between the marginal processes. Large values of
, which determines the degree of dependence between the marginal processes. Large values of  correspond to strong dependence, small values to weak dependence.
correspond to strong dependence, small values to weak dependence.
Contributed by: Andrzej Kozlowski (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Most applications of financial processes, particularly in finance, require multidimensional models (e.g. basket options, portfolio optimization, etc.). This is not a major obstacle as long as one stays within the framework of diffusion processes driven by a (multidimensional) Brownian motion, since in this case the dependence structure is characterized in terms of correlation matrices. However, the situation is more complicated in the case of models that include discontinuous jumps.
The simplest way to introduce jumps into multidimensional models is to take a multivariate Brownian motion and "time-change" it with a univariate subordinator (see the related Demonstration in the Related Links section). However, the range of dependence patterns obtained in this way is quite limited and, in particular, does not include independence. A much more sophisticated approach developed in [2] is based on the concept of a Lévy cupola. Here we illustrate this approach by using a simple example taken from [1] (Example 6.18). The components of the process are two  -stable subordinators, that is, self-similar Lévy processes with positive jumps, whose distributions are stable distributions with stability index
-stable subordinators, that is, self-similar Lévy processes with positive jumps, whose distributions are stable distributions with stability index  (stability index 2 gives the Gaussian distribution). The Lévy measure of such processes has a particularly simple form. The Lévy copula used is the Clayton–Lévy copula. In this setting the general algorithm given in [1] for simulating multidimensional Lévy processes whose dependence structure is given by a Lévy copula can be carried out very efficiently, which is why we chose this case for this Demonstration.
(stability index 2 gives the Gaussian distribution). The Lévy measure of such processes has a particularly simple form. The Lévy copula used is the Clayton–Lévy copula. In this setting the general algorithm given in [1] for simulating multidimensional Lévy processes whose dependence structure is given by a Lévy copula can be carried out very efficiently, which is why we chose this case for this Demonstration.
[1] R. Cont and P. Tankov, Financial Modelling with Jump Processes, New York: CRC Press, 2004.
[2] J. Kallsen and P. Tankov, "Characterization of Dependence of Multidimensional Lévy Processes Using Lévy Copulas," Journal of Multivariate Analysis, 97(7), 2006 pp. 1551–1572.
Permanent Citation