Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Cosinor Analysis Using Rotating Ellipse Tangents and Circle Collisions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

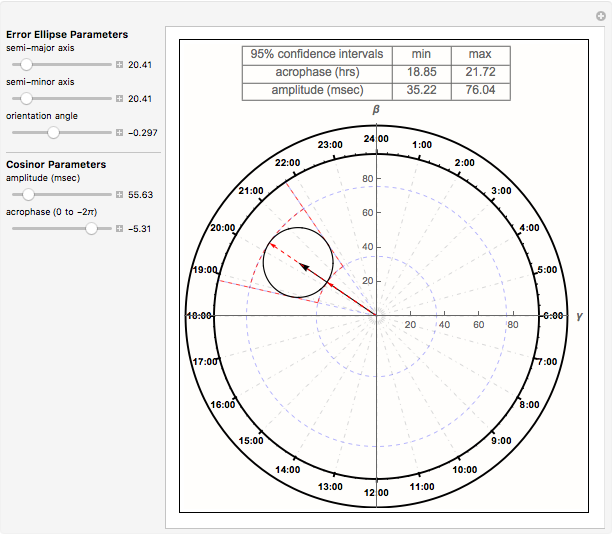
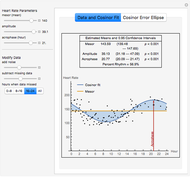
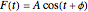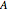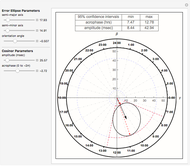
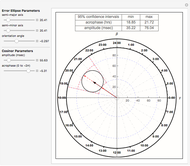
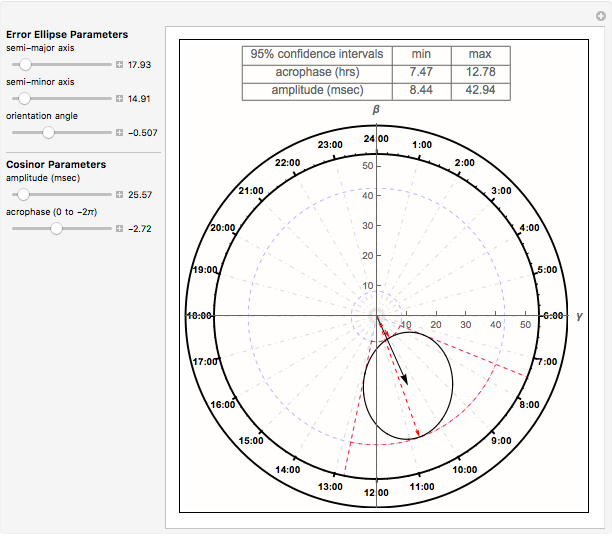
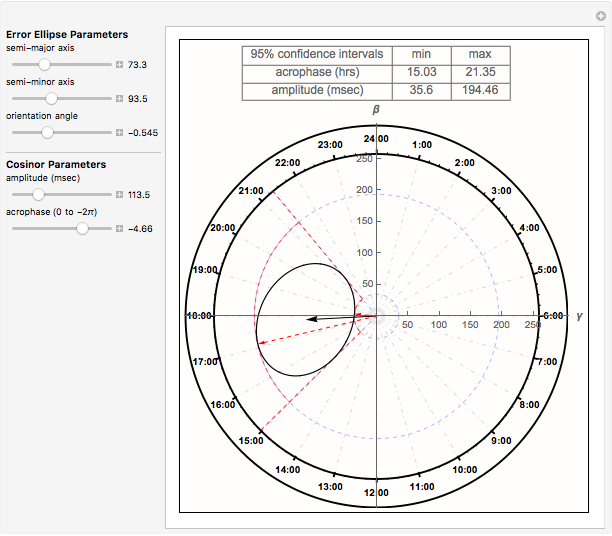
Cosinor analysis uses a least squares method to fit a cosine wave to biorhythm time series data. The method can be applied to nonuniformly sampled studies with missing data points. The fitted cosine function is given by , where is the amplitude and is the acrophase of the time series [1], [2]. The acrophase is the time period in which the cycle peaks. The Demonstration plots the cosinor 95% bivariate error ellipse of the cosinor parameter estimates and dynamically computes associated confidence interval (CI) limits.

[more]

In the bookmarks, data is shown from cosinor analysis of 24-hour heart rate (HR) recordings in humans. HR is reported by its reciprocal parameter, RR interval, the time between consecutive heartbeats measured in milliseconds. Illnesses such as heart disease and depression disturb the amplitude and acrophase of 24-hour HR periodicity.

[less]

Contributed by: Erik Mahieu and Forrester A. Lee (February 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

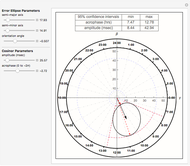
Using coordinate geometry analysis to characterize tangency conditions and circle-ellipse collisions, Mathematica root-solving methods are applied dynamically to determine acrophase and amplitude confidence interval (CI) limits. The cosinor error ellipse parametric curve, 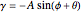and 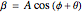, lies on the axis of the acrophase angle () offset by a tilt (). Cosinor studies with uneven and/or missing data produce a rotated, eccentric ellipse, which influences CI limits.

References

[1] M. A. Rol de Lama, J. P. Lozano, V. Ortiz, F. J. Sánchez-Vázquez, and J. A. Madrid, "How to Engage Medical Students in Chronobiology: An Example on Autorhythmometry," Advances in Physiology Education, 29, 2005 pp. 160–164. advan.physiology.org/content/29/3/160.full.pdf+html.

[2] R. Ferrara and A. Antonellini, "Using the SAS System for COSINOR Analysis of 24 Hour Ambulatory Blood Pressure Monitoring (ABPM) Data," in SAS European Users Group International Proceedings (SEUGI 1993), Jersey, Channel Islands: SAS Institute, 1993. www.sascommunity.org/seugi/SEUGI1993/Using%20 the %20 SAS %20 System %20 for %20 COSINOR %20 Analysis %20 of %2024 %20 Hour %20 Ambulatory %20 Blood %20 Pressure %20 Monitoring %20(ABPM)%20 Data.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send