Cotes Identity

Initializing live version

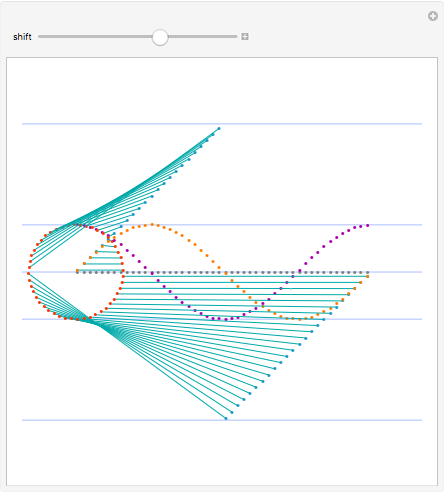
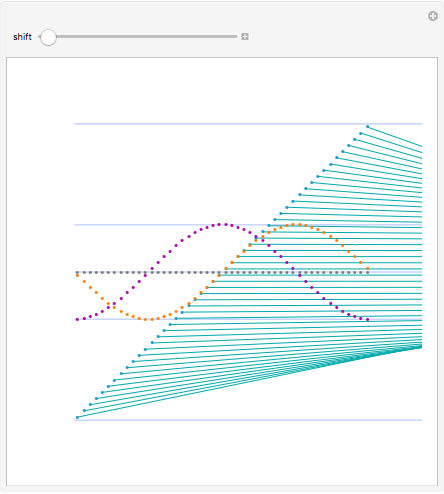
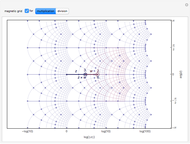
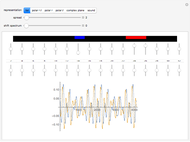
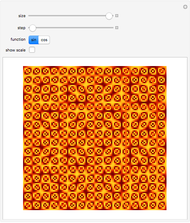
Cotes published in 1714 that 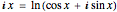. Shift the range of to explore the exponential relationship between cosine and sine.

Contributed by: Michael Schreiber (March 2011)
Open content licensed under CC BY-NC-SA

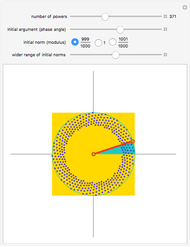
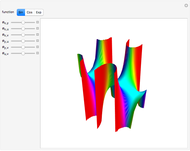
Snapshots

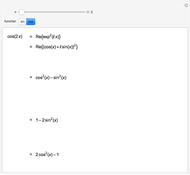
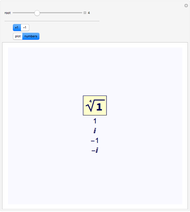
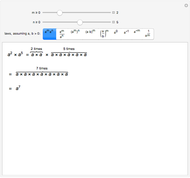
Note that 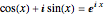for all , but 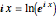only for 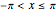when 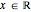. Outside of this range the relation is for some integer value of .


Feedback (field required)

Email (field required)	Name

Occupation	Organization

Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback. Send