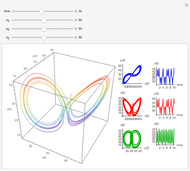
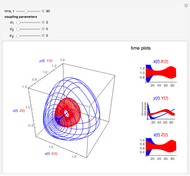
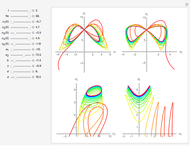
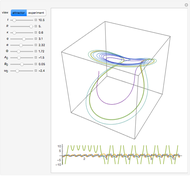
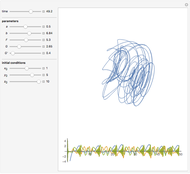
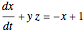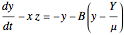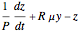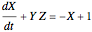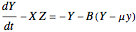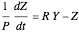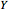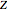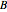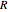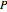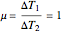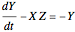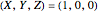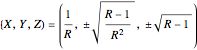Coupled Lorenz Oscillators
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
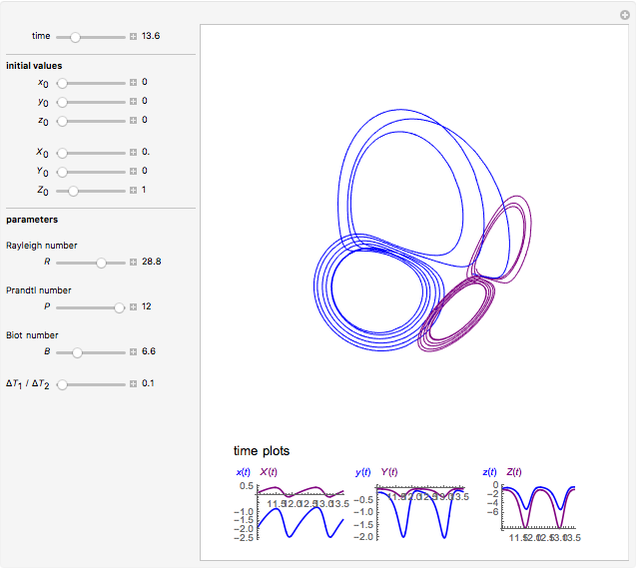
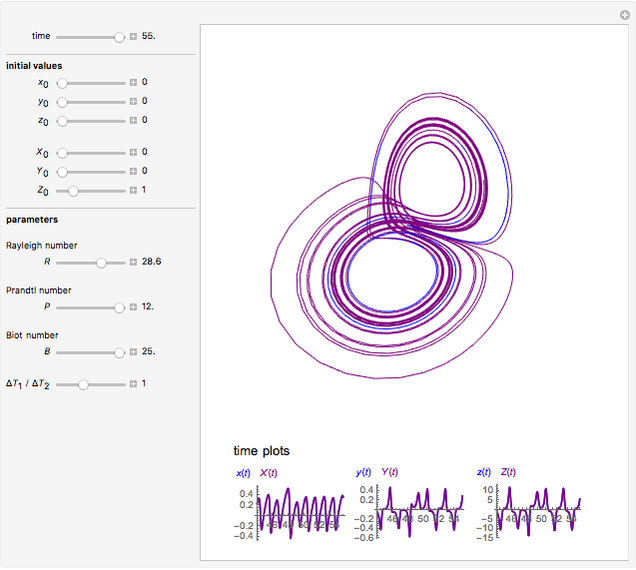
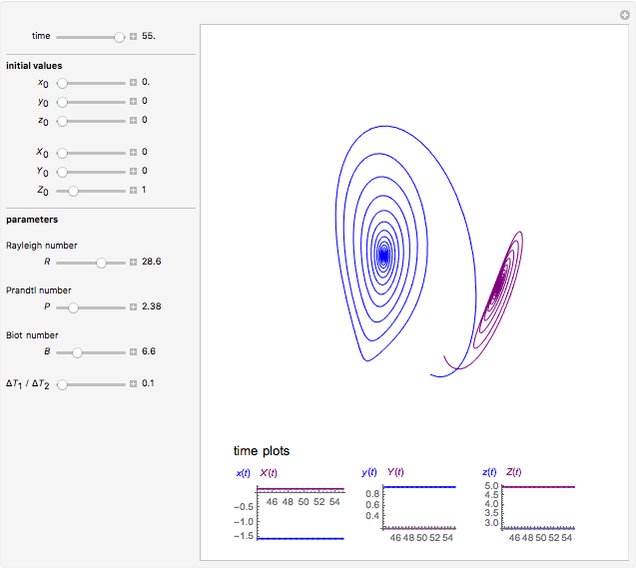
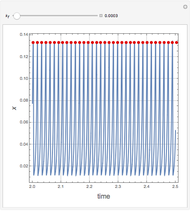
This Demonstration simulates the dynamics of two thermally coupled thermosiphons.
[more]
Contributed by: Clay Gruesbeck (March 2013)
Open content licensed under CC BY-NC-SA
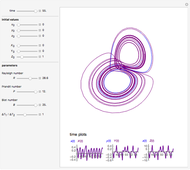
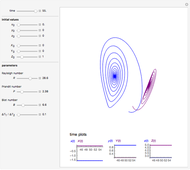
Snapshots
Details
References
[1] S. H. Davis and M. N. Roppo, "Coupled Lorenz Oscillators," Physica D, 24(1–3), 1987 pp. 226–242. doi:10.1016/0167-2789(87)90077-7.
[2] C. Sparrow, The Lorenz Equations: Bifurcation, Chaos, and Strange Attractors, New York: Springer, 1982.
Permanent Citation