Coupled Quantum Harmonic Oscillators

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
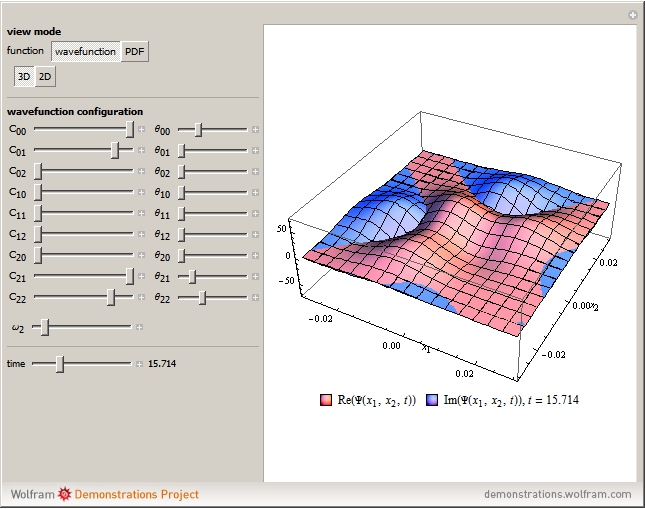
This Demonstration models a coupled system of quantum harmonic oscillators with two electron masses in SI units; two particles have displacements  and
and  from their equilibrium points. The outer springs have an angular frequency
from their equilibrium points. The outer springs have an angular frequency  and the inner spring an angular frequency
and the inner spring an angular frequency  , which can be varied. Thus, the potential energy term of the Hamiltonian is
, which can be varied. Thus, the potential energy term of the Hamiltonian is  .
.
Contributed by: Humberto Munoz Bauza (September 2013)
After work by: Rachael M. McDermott and Ian H. Redmount
(Mathematica Summer Camp 2013)
Open content licensed under CC BY-NC-SA
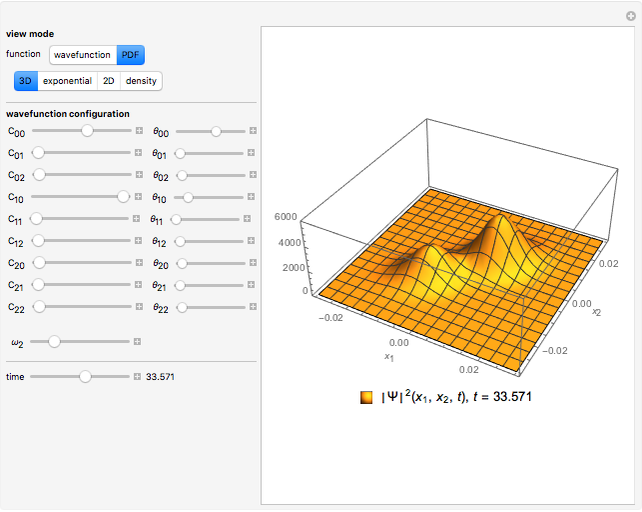
Snapshots
Details
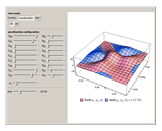
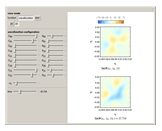
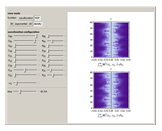
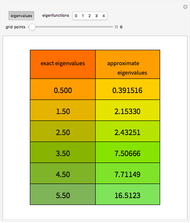
The plots are
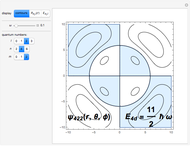
• 3D wavefunction plots with their real and complex parts
• wavefunction real and complex density plots
• 3D PDF plots
• cross sectional plots of the PDF plot at its expectation value (with the cross section planes orthogonal to the  and
and  axes)
axes)
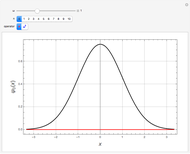
• PDFs of the  and
and  displacements
displacements
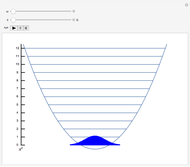
• density plots of the  and
and  displacements over time
displacements over time
Reference
[1] R. M. McDermott and I. H. Redmount, "Coupled Classical and Quantum Oscillators." arxiv.org/abs/quant-ph/0403184v2.
Permanent Citation