Cyclic Staircase versus Cyclic Voltammetry for Reversible Electron Transfer Reaction

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
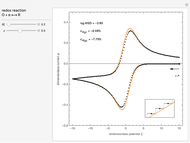
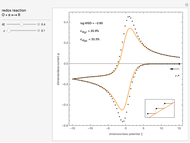
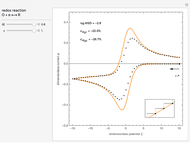
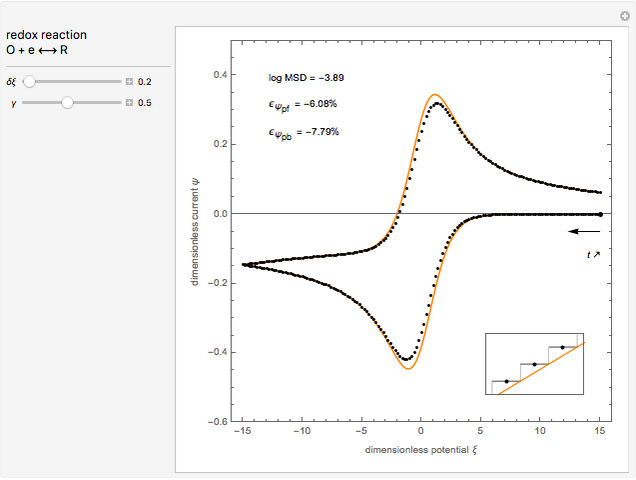
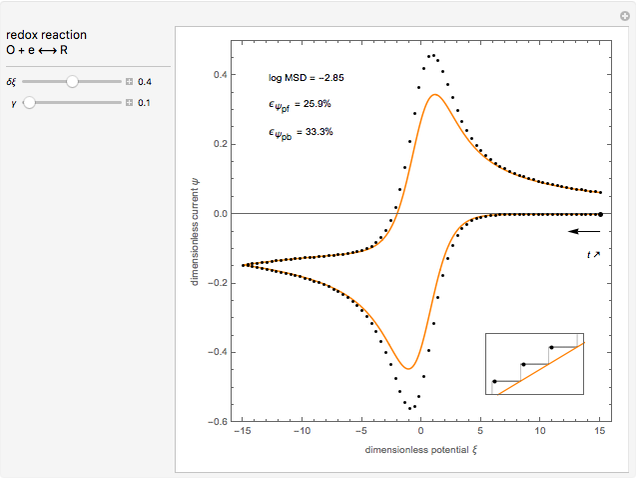
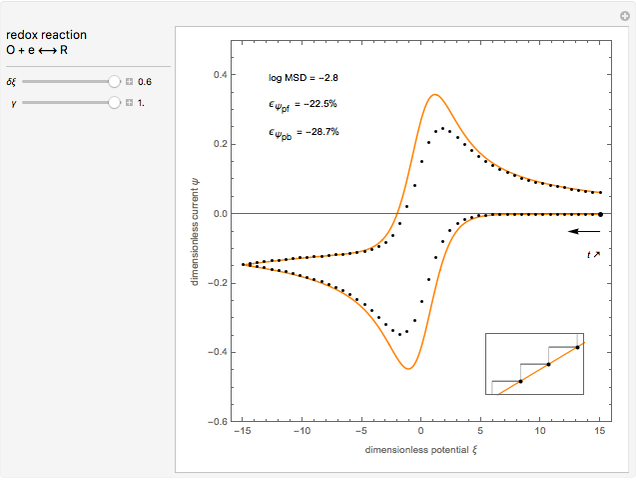
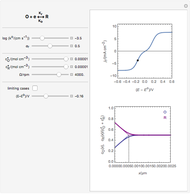
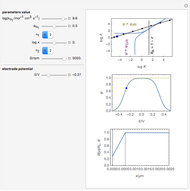
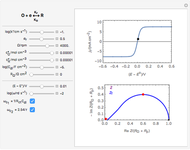
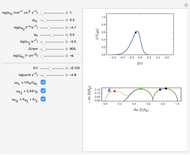
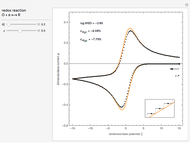
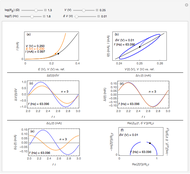
This Demonstration models the voltammetric response (black dots) for a reversible electron transfer reaction taking place at the surface of a planar macroelectrode, with cyclic staircase perturbation of the electrode potential (black staircase in the inset). The sampled staircase voltammetric response (black dots) is compared to the electrode response (orange line) obtained by application of a cyclic potential ramp (orange line in the inset). The model assumes semi-infinite diffusion of redox species normal to the electrode surface. You can experiment with the effects of the amplitude of potential step for the staircase signal, and the sampling condition for evaluation of the current response, using the controls for the dimensionless parameters 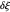 and
and 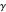 . The plots show the dimensionless current density
. The plots show the dimensionless current density 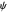 as a function of the dimensionless potential
as a function of the dimensionless potential  . The relative deviations
. The relative deviations 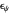 for the peak forward (pf) and peak reverse (pr) reactions for the two voltammograms are displayed, as well as the mean squared deviation (MSD).
for the peak forward (pf) and peak reverse (pr) reactions for the two voltammograms are displayed, as well as the mean squared deviation (MSD).
Contributed by: Claude Montella and Jean-Paul Diard (July 2017)
(Univ. Grenoble Alpes, LEPMI, Grenoble, France)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Cyclic voltammetry (CV) is widely used for investigating electrochemical reactions [1]. The input signal for CV is a sawtooth potential signal, with slope (scan rate) 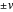 . Computer-controlled digital instruments cannot apply true linear ramps. A staircase potential signal is employed in practice, which results in the cyclic staircase voltammetry (CSCV) technique. Each potential step of the staircase signal involves three parameters: the amplitude
. Computer-controlled digital instruments cannot apply true linear ramps. A staircase potential signal is employed in practice, which results in the cyclic staircase voltammetry (CSCV) technique. Each potential step of the staircase signal involves three parameters: the amplitude 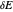 , the time interval
, the time interval 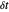 following the potential step and the time
following the potential step and the time 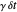 where the current is sampled/measured. The parameter
where the current is sampled/measured. The parameter 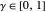 is the sampling ratio for CSCV. The staircase signal results in a formal potential scan rate,
is the sampling ratio for CSCV. The staircase signal results in a formal potential scan rate, 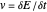 . A general theory for pulse voltammetry techniques, and in particular for CSCV, can be found in [2].
. A general theory for pulse voltammetry techniques, and in particular for CSCV, can be found in [2].
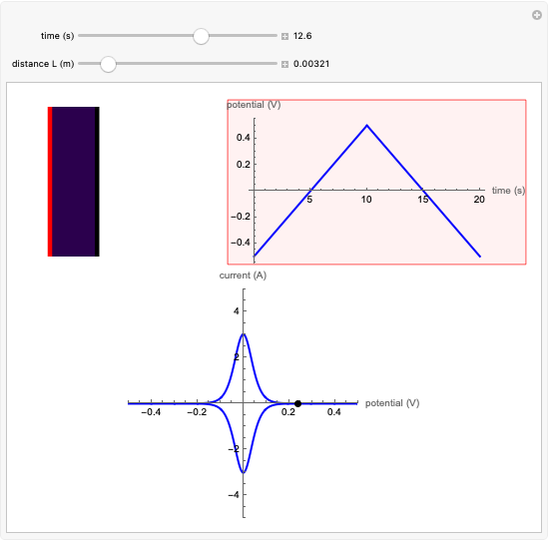
The Demonstration focuses on the electrochemical reaction, 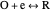 , involving two soluble species. The model assumes reversible electron transfer kinetics at the electrode surface and semi-infinite linear diffusion of redox species in the electrolyte. The species
, involving two soluble species. The model assumes reversible electron transfer kinetics at the electrode surface and semi-infinite linear diffusion of redox species in the electrolyte. The species  is absent at the initial time. The CV response is the orange line. The CSCV response sampled at
is absent at the initial time. The CV response is the orange line. The CSCV response sampled at  , for
, for 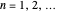 , is shown by the black dots. The graphical inset shows the first steps of the staircase signal, together with the sampling times (dots) and the linear potential ramp (orange line) with slope
, is shown by the black dots. The graphical inset shows the first steps of the staircase signal, together with the sampling times (dots) and the linear potential ramp (orange line) with slope 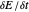 . Dimensionless notation is used for the electrode potential
. Dimensionless notation is used for the electrode potential 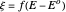 , the current density
, the current density 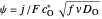 , and the amplitude of the potential step
, and the amplitude of the potential step 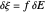 for the CSCV technique. Here
for the CSCV technique. Here 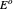 is the standard potential of redox couple,
is the standard potential of redox couple, 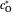 is the initial concentration of reactant,
is the initial concentration of reactant, 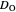 is its diffusion coefficient and
is its diffusion coefficient and 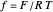 is the Nernst constant,
is the Nernst constant, 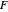 ,
, 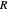 and
and 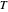 having their usual meaning. By way of illustration, setting
having their usual meaning. By way of illustration, setting 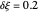 , the potential step amplitude is
, the potential step amplitude is 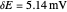 at 25 °C, and the time length following each potential step is
at 25 °C, and the time length following each potential step is 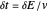 .
.
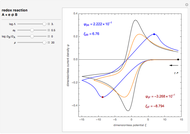
The main purpose of this Demonstration is to exhibit the optimal sampling condition that guarantees the equivalence of CSCV and CV current data within an acceptable error. Two criteria are used here: first, the relative deviation ( ) between the voltammetric peak (subscript
) between the voltammetric peak (subscript 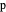 ) currents for the forward (subscript
) currents for the forward (subscript  ) and backward (subscript
) and backward (subscript 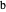 ) potential scans, and second, the mean squared deviation (MSD) between the two voltammograms. Computational details can be found in [3].
) potential scans, and second, the mean squared deviation (MSD) between the two voltammograms. Computational details can be found in [3].
References
[1] A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, 2nd ed., New York: Wiley, 2001.
[2] Á. Molina, and J. González, Pulse Voltammetry in Physical Electrochemistry and Electroanalysis: Theory and Applications, Cham: Springer International Publishing Switzerland, 2016.
[3] C. Montella, "Further Investigation of the Equivalence of Staircase and Linear Scan Voltammograms. I- Sampling Conditions for Reversible Reactions Involving Soluble Species," Journal of Electroanalytical Chemistry, 796, 2017 pp. 96–107. doi:10.1016/j.jelechem.2017.04.048.
Permanent Citation