Cycloid Curves

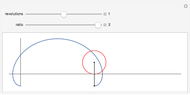
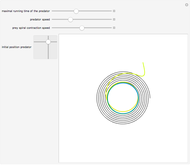
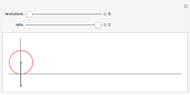
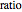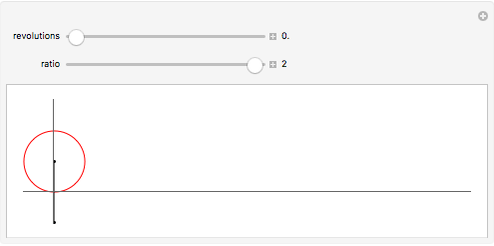
The curve traced out by a point on the rim of a circle rolling along a straight line is called a cycloid. Let the radius of the circle be . Allowing the tracing point to be either within or without the circle at a distance from the center generates "curtate" or "prolate" cycloids, respectively. The variable is 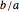, limited to the range [0, 2]. For 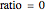, the result is a straight horizontal line. 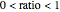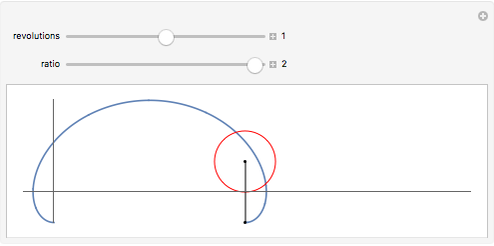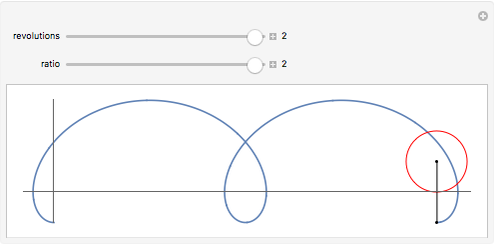For , the curve is a curtate cycloid. For 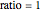, it is an ordinary cycloid. For , it is a prolate cycloid. Note that 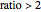is allowable but not used here.