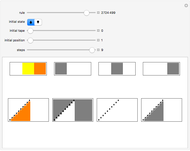
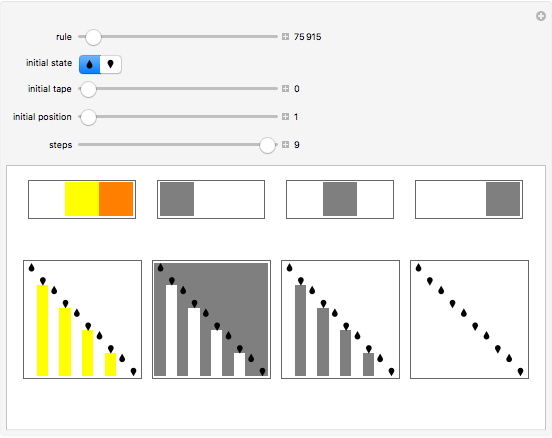
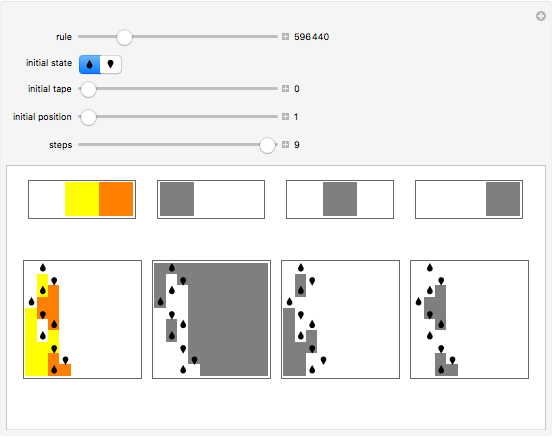
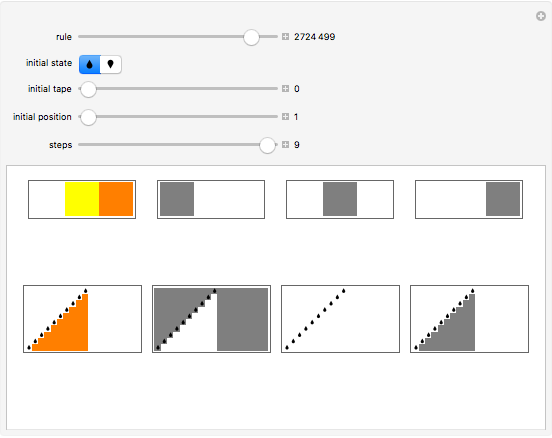
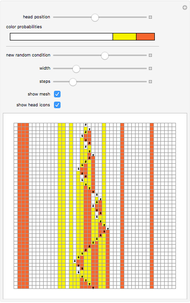
Decomposition of 2,3 Turing Machine Evolutions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
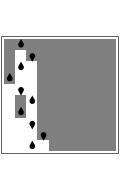
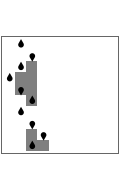
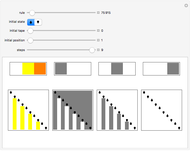
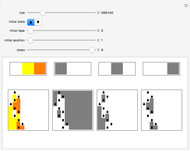
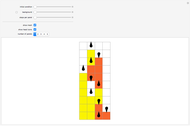
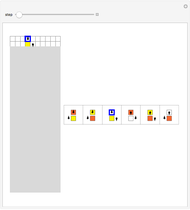
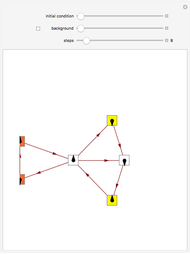
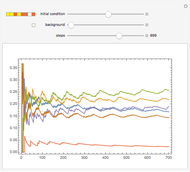
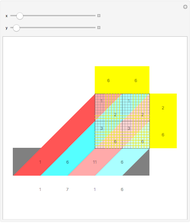
Turing machines are simple models of a computing machine invented by Alan Turing. They consist of a head that switches between states while reading from and writing on a tape. The symbols read or written are called colors. Generalizations of such machines can have multiple heads or tapes.
[more]
Contributed by: Michael Schreiber (March 2011)
Open content licensed under CC BY-NC-SA
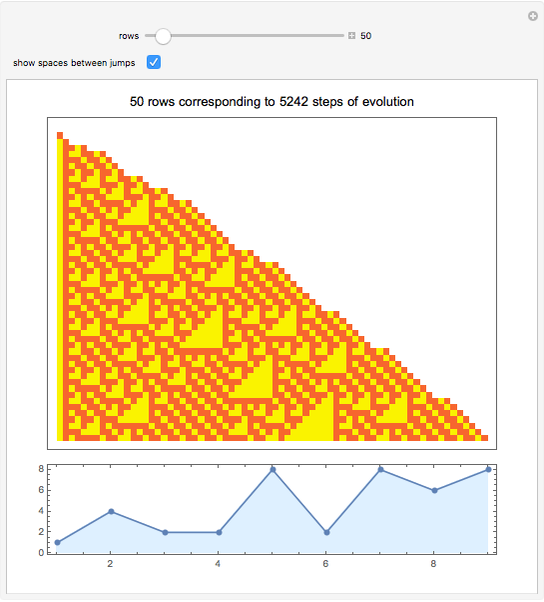
Snapshots
Details
detailSectionParagraphPermanent Citation
"Decomposition of 2,3 Turing Machine Evolutions"
http://demonstrations.wolfram.com/DecompositionOf23TuringMachineEvolutions/
Wolfram Demonstrations Project
Published: March 7 2011