Decomposition of a Rhombic Dodecahedron

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
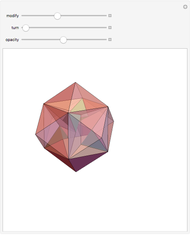
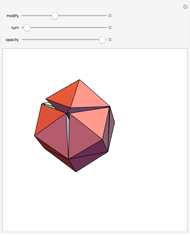
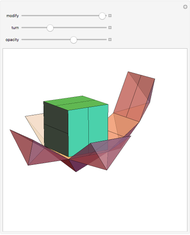
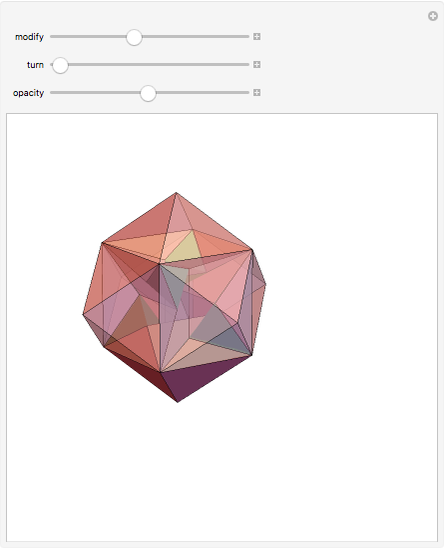
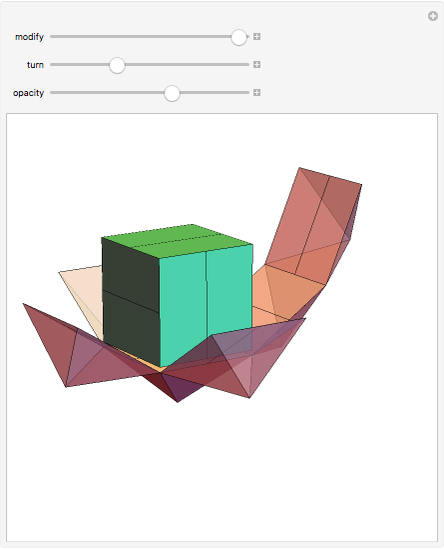
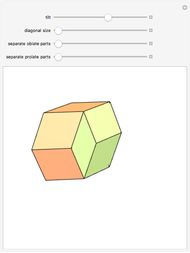
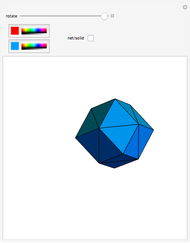
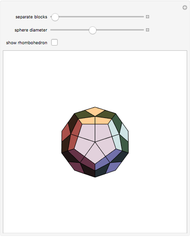
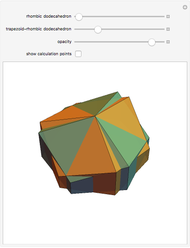
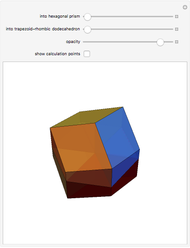
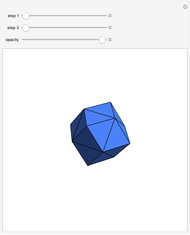
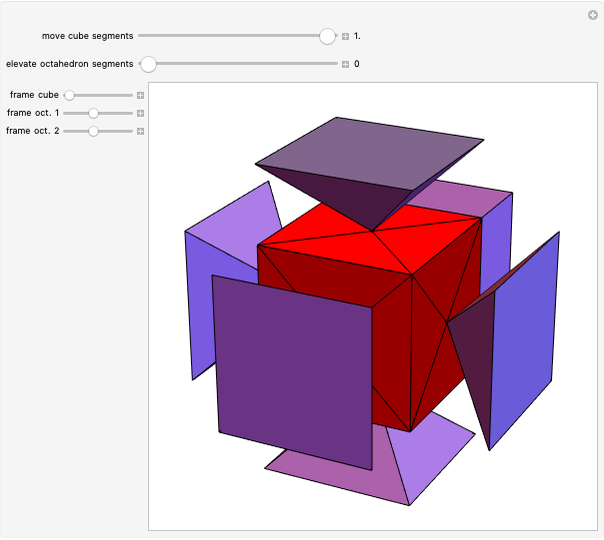
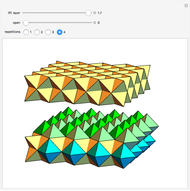
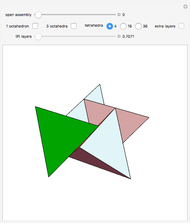
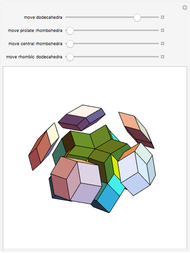
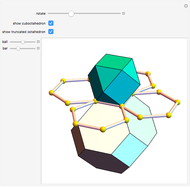
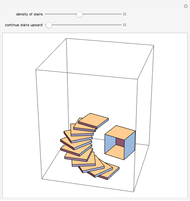
A rhombic dodecahedron can be decomposed into a cube and six smaller, mutually congruent pieces, which can be reassembled to form a second cube of the same size as the first. In other words, the rhombic dodecahedron can be equidissected into two cubes of equal size. Furthermore, these cubes can be simultaneously modified so that the ratio of their volumes continuously varies between the extremes of 0:1 and 1:1.
[more]
Contributed by: Lajos Szilassi, Gábor Gévay, and Sándor Kabai (January 2012)
Open content licensed under CC BY-NC-SA
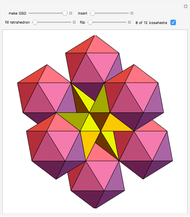
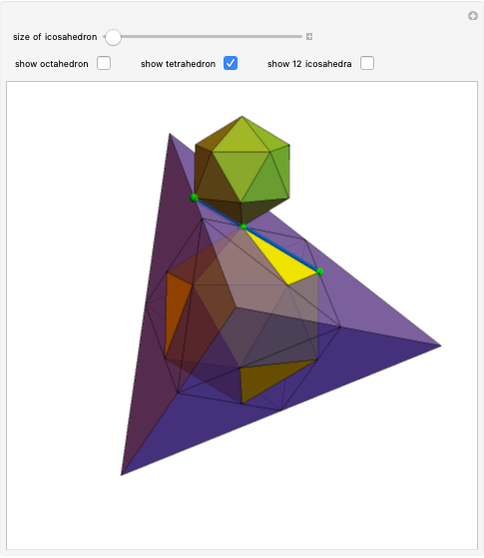
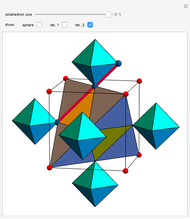
Snapshots
Details
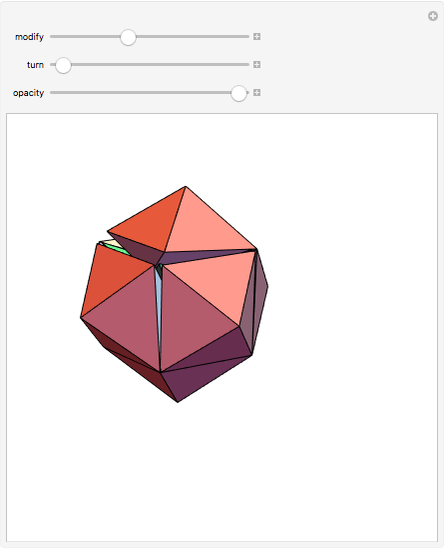
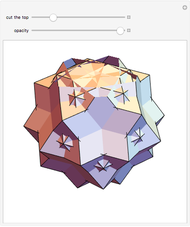
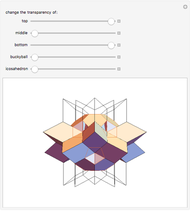
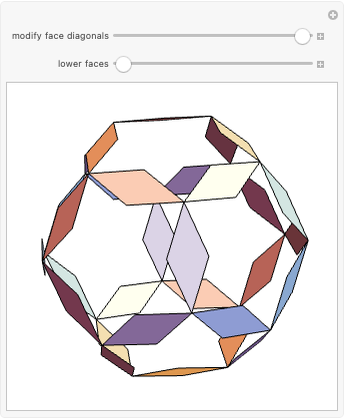
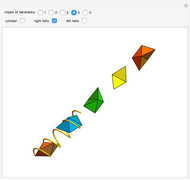
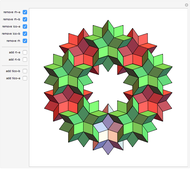
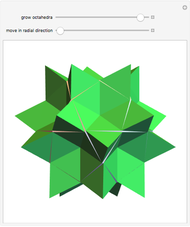
In general, the two complementary blocks take the shape of a concave and a convex pentagonal dodecahedron, respectively. Both exhibit the symmetry of a pyritohedron, which is a polyhedron bounded by 12 axially symmetric (but not regular) convex pentagons (the crystal form of the sulfur mineral pyrite). This symmetry is determined by three mutually perpendicular mirror planes and four three-fold rotation axes (the direction of these axes is that of the four body diagonals of the cube). Hence, it is less than the symmetry of the regular pentagonal dodecahedron. However, there is an intermediate stage when the second block takes on just this latter, regular shape. On the other hand, in the extreme case corresponding to the volume ratio 0:1, the symmetry is that of the cube. In this case, the first block degenerates to a quadruple of line segments passing through a common point (in fact, the quadruple of the body diagonals of the cube). The second block, in turn, becomes a rhombic dodecahedron congruent to the starting figure. Thus, one sees how a rhombic dodecahedron can be decomposed into six equal tetragonal bipyramids with a common apex; then, after a half-turn of each, they reassemble to form another rhombic dodecahedron ("turning the rhombic dodecahedron inside out").
The continuous change of the shape of the two blocks described above is illustrated by a nice series of figures in [1].
Our Demonstration can be considered as another illustration of the transformation of polyhedral shapes described by Branko Grünbaum.
Reference
[1] B. Grünbaum, "Acoptic Polyhedra," in Advances in Discrete and Computational Geometry: Proceedings of the 1996 AMS-IMS-SIAM Joint Summer Research Conference, South Hadley, MA (B. Chazelle, J. E. Goodman, and R. Pollack, eds.), Providence, RI: American Mathematical Society, 1996 pp. 163–199.
Permanent Citation
"Decomposition of a Rhombic Dodecahedron"
http://demonstrations.wolfram.com/DecompositionOfARhombicDodecahedron/
Wolfram Demonstrations Project
Published: January 5 2012