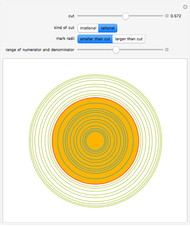
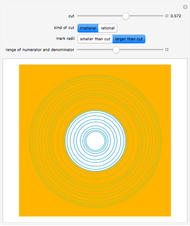
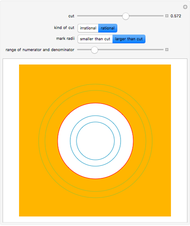
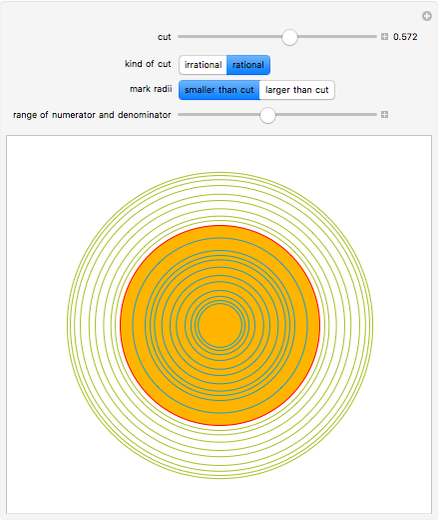
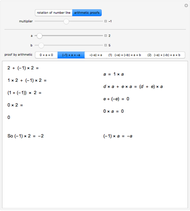
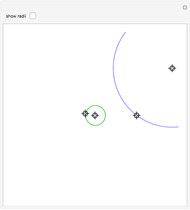
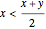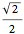Split the rationals in two disjoint sets A and B, such that all the elements of A are smaller than all the element of B. This is called a cut. There are four cases: A has a largest element or not, and B has a smallest element or not.
The case where A has a largest element x and B has a smallest element y is impossible. On the one hand, the average of x and y, being a rational, must belong to one of A or B. On the other hand, their average cannot belong to A (because 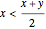 ) nor to B (because
) nor to B (because  ).
).
If there is a largest element of A or a smallest element of B, then the cut is rational.
In the fourth case, the most interesting one, A does not have a largest element and B does not have a smallest element. In that case the cut is irrational.
This visualization draws circles with rational radii smaller than 1. Examples of rational cuts are selected from these, with a red circle used to indicate that the rational is included in one of the two sets. Examples for irrational cuts are generated as multiples of 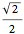 .
.
[less]