Deformation of Noncylindrical Compression Springs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
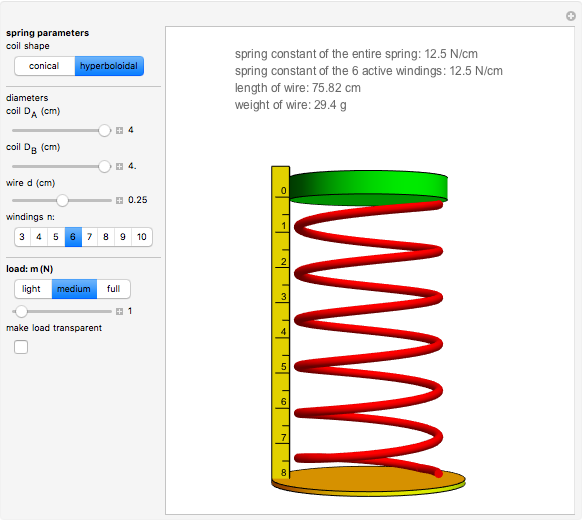
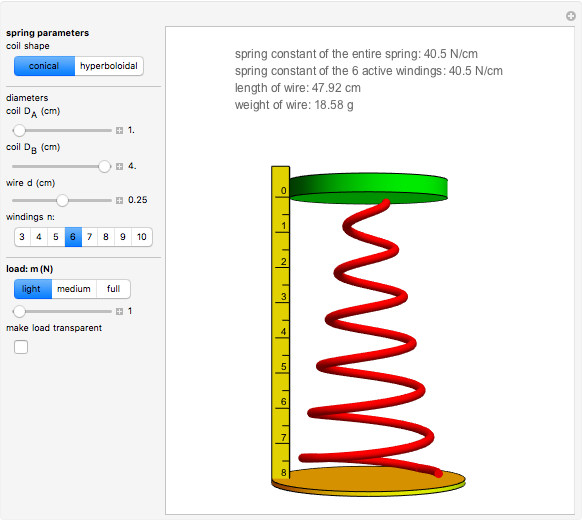
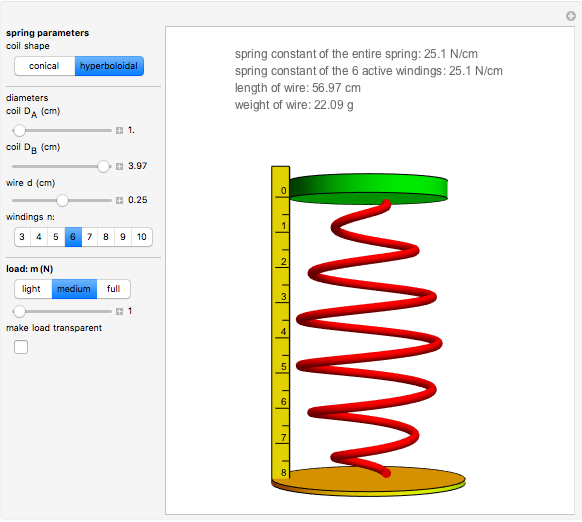
This Demonstration models the deformation of a noncylindrical spring under a compression load. A compression spring is designed to get shorter when a load is applied to it. Examples are vehicle suspension springs, mattress and upholstery springs, and springs used in switches, controllers, and so on. Many compression springs are cylindrical in shape but others are conical (tapered) or hyperboloidal (hourglass/barrel) with a variable coil diameter. One advantage of noncylindrical springs is that their spring constant varies during compression. The larger diameter coil windings collapse and become inactive first, followed step by step by the smaller diameter windings, thus keeping the action of the spring constant. Another advantage of shaped springs compared to cylindrical ones is that higher effective spring constants can be attained with less voluminous springs, requiring wire of a smaller diameter. Typical examples are the hourglass shaped (Bonnell) springs in mattresses. If the mattress were made out of cylindrical springs with the same spring constant and covering the same area, its weight would be prohibitive. Bonnell springs combine large volume and light weight with large effective spring constants. These springs are soft (low spring constant) under a relatively light load. They get harder (higher spring constant) as the load increases when the larger diameter windings have collapsed.
Contributed by: Erik Mahieu (June 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The formula for the spring constant of a helical spring with constant pitch and constant winding diameter adapted for steel wire is: 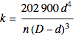 N/cm, where
N/cm, where 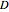 is the coil diameter,
is the coil diameter,  is the wire diameter, and
is the wire diameter, and  is the number of active windings.
is the number of active windings.
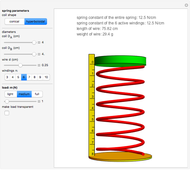
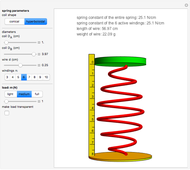
An active winding is a winding that has not been collapsed (has height larger than the wire diameter). In a cylindrical spring, under increasing load, all windings collapse simultaneously, but in shaped springs this is not the case. Conical springs have their windings collapse in sequence, one at a time, from large to small diameters. For hyperboloidal springs, the larger windings collapse first in groups of two (except in the case of an odd number of windings when the smallest one will collapse last by itself).
A shaped spring is taken as a stack of cylindrical springs with varying outer diameters. The effective spring constant 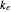 is then that of a set of springs in series and the result of the formula:
is then that of a set of springs in series and the result of the formula: 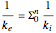 . For the springs in this Demonstration, this is:
. For the springs in this Demonstration, this is: 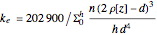 where
where 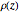 represents the radius of the spring winding in the function of its position along its central axis.
represents the radius of the spring winding in the function of its position along its central axis.
Snapshots 1, 2, and 3: These are the cylindrical, conical, and barrel-shaped versions of the spring in the thumbnail. All have the same free height, number of windings, wire diameter, and maximum coil diameter. Only their coil shapes are different. Look at the differences in the spring constant, load needed to get approximately the same deflection, weight, and length of wire used.
Snapshots 4, 5, and 6: The same three springs as Snapshots 1, 2, and 3 but now fully compressed to their "solid height". Again, there is a big difference between the cylindrical and shaped versions.
Snapshots 7, 8, and 9: These show how in the cylindrical spring all windings deform equally and collapse simultaneously and how the windings of the shaped springs deform differently and collapse sequentially.
Permanent Citation