Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Dehn Invariant of Some Disjoint Unions of Polyhedra with Octahedral Symmetry

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

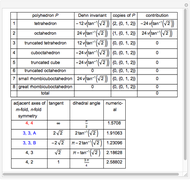
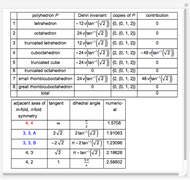
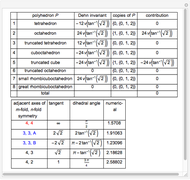
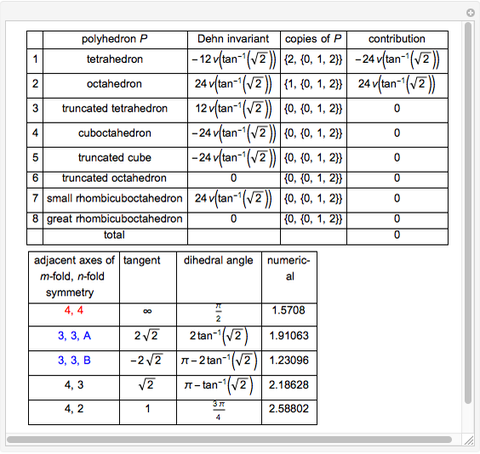
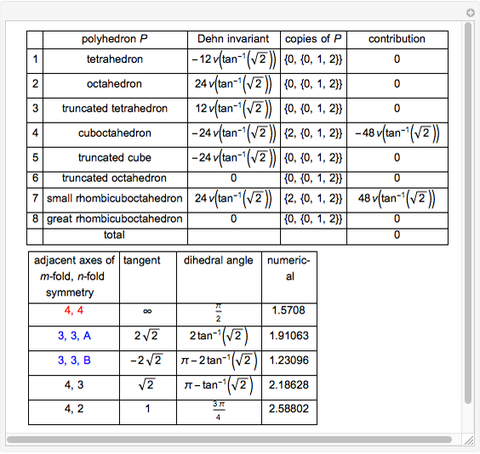
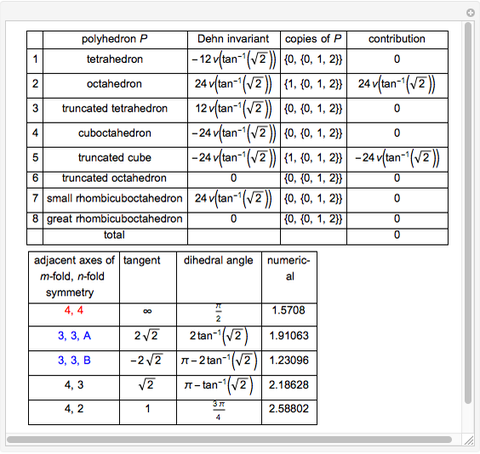
The Dehn invariant of a polyhedron is 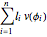, where 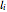is the length of the edge , is the corresponding dihedral angle, and is an additive functional defined on a certain finite-dimensional vector space of reals over the rationals for which [1]. A polyhedron has Dehn invariant 0 if and only if it is equidecomposable with a cube of same volume.

[more]

This Demonstration calculates Dehn invariants for disjoint unions of Platonic and Archimedean solids having octahedral symmetry (and edge length 1). In this case, the dihedral angles are supplementary to the angles between suitable axes of rotational symmetry.

The disjoint union of a tetrahedron and a truncated tetrahedron has Dehn invariant 0.

[less]

Contributed by: Izidor Hafner (October 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

That some combinations of Platonic and Archimedean solids have Dehn invariant 0 was shown in [1].

Reference

[1] J. H. Conway, C. Radin, and L. Sadun, "On Angles Whose Squared Trigonometric Functions Are Rational," Discrete & Computational Geometry, 22(3), 1999 pp. 321–332. doi:10.1007/PL00009463.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send