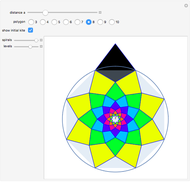
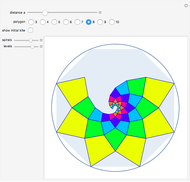
Deltoid Kite Tiling

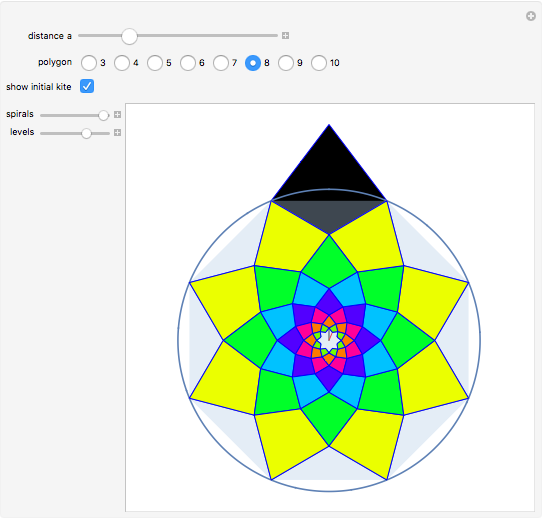
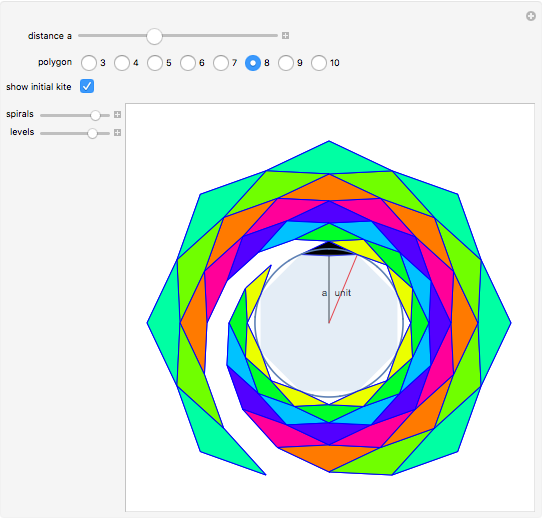
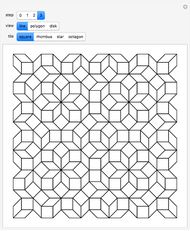
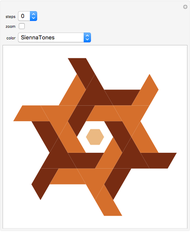
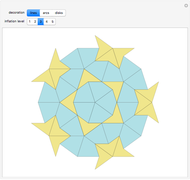
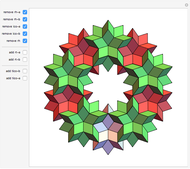
Construct an initial kite so that two of its vertices coincide with two adjacent vertices of a regular polygon constructed on the unit circle. Let the other two vertices of the kite be on a radius bisecting that side of the polygon, one at an arbitrary distance from the origin, and the other at a distance so that the different sides of the deltoid are in the ratio . Now place copies of this kite on each edge of the polygon, and tile the plane inside or outside the polygon with kites having sizes decreased or increased in proportion to .