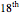Densest Tetrahedral Packing

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
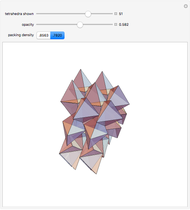
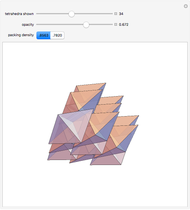
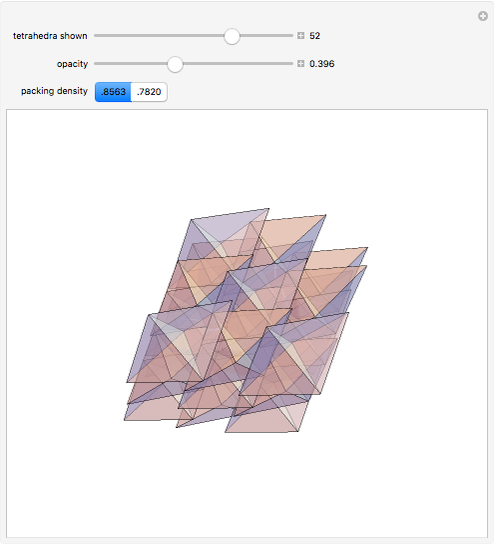
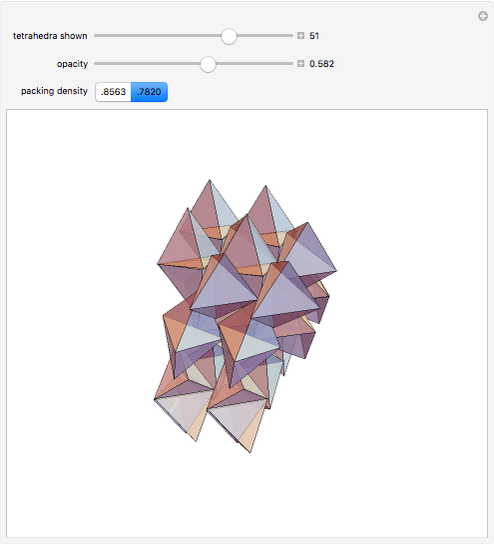
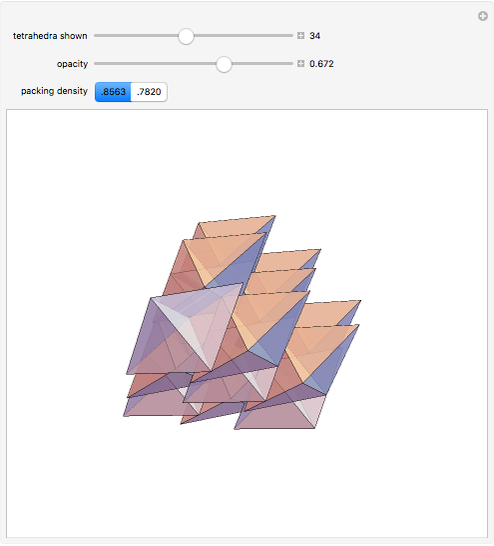
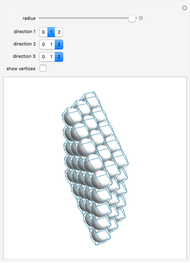
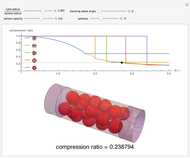
Obsolete news: The cover article for the 13 August 2009 issue of Nature published a packing method for tetrahedra with a packing density of 0.782021, a new record. For complex packings, space is divided into an orderly arrangement of identical cells. In this packing, each cell has 72 tetrahedra, shown here.
[more]
Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] S. Torquato and Y. Jiao, "Dense Packings of the Platonic and Archimedean Solids," Nature, 460(13), 2009 pp. 876–879.
[2] Supplementary Information.
[3] E. Chen, M. Engel, and S. Glotzer, "Dense Crystalline Dimer Packings of Regular Tetrahedra," Discrete and Computational Geometry, 44(2), 2010 pp. 253–280. http://arxiv.org/abs/1001.0586.
Permanent Citation
"Densest Tetrahedral Packing"
http://demonstrations.wolfram.com/DensestTetrahedralPacking/
Wolfram Demonstrations Project
Published: March 7 2011