Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

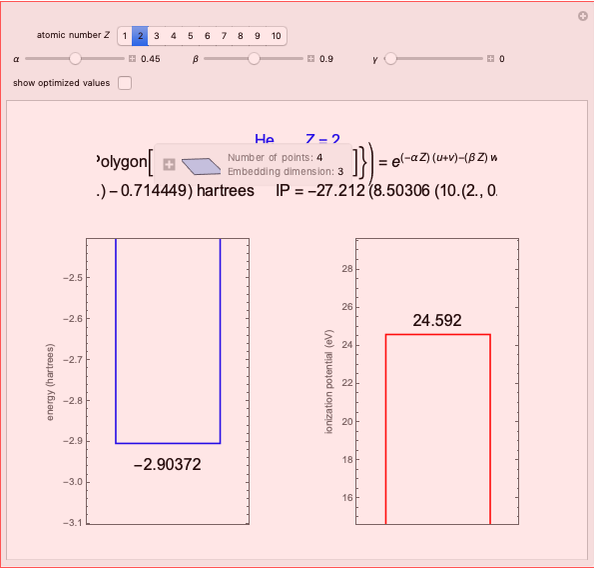
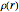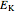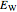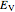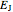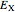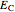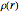Density Functional Computations on Noble Gas Atoms

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

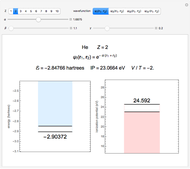
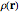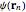Density functional theory (DFT) has now become the predominant technique in computational quantum chemistry, having displaced wavefunction-based computations for atoms, molecules and solids. The key reason is that QFT deals with a single electron density function for an -electron system, rather than a complicated combination of orbital functions . The fundamental validity of DFT and its practical implementation by a variational principle are expressed in two theorems of Hohenberg and Kohn. For all necessary background on DFT, refer to the definitive monograph of Parr and Yang [1]. For more recent advances, see also [2].

[more]

In this Demonstration, a modified version of DFT is applied to compute the energies and electron distributions of the noble-gas atoms He, Ne, Ar, Kr and Xe. The energy functional of the spherically symmetric density consists of the following parts: the kinetic energy , the Weizsäcker correction , the electron-nuclear potential energy , the interelectronic Coulomb energy , the Dirac exchange energy and finally, the correlation energy , for which a novel form is suggested. The density functional is designed to take account of the shell structure of the atom, following a computation of Wang and Parr [3], as well as a curve fitting by the author [4].

You can select values for the one or more exponential parameters to optimize the total energy and the radial distribution function. In principle, the exact nonrelativistic energies of the noble gas atoms can be reproduced, with the exception of the helium atom, which has too few electrons for a successful statistical model. The default values are chosen to be very close to optimal, to simplify your task.

[less]

Contributed by: S. M. Blinder (June 2019)
Open content licensed under CC BY-NC-SA

Details

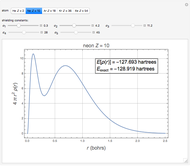
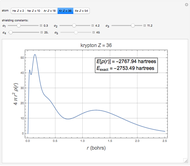
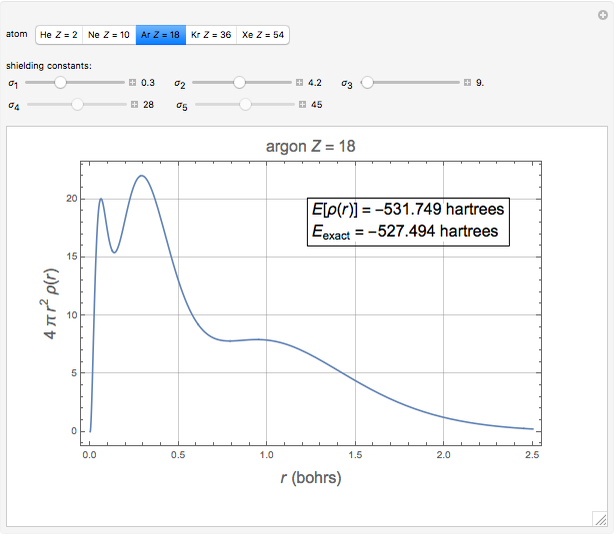
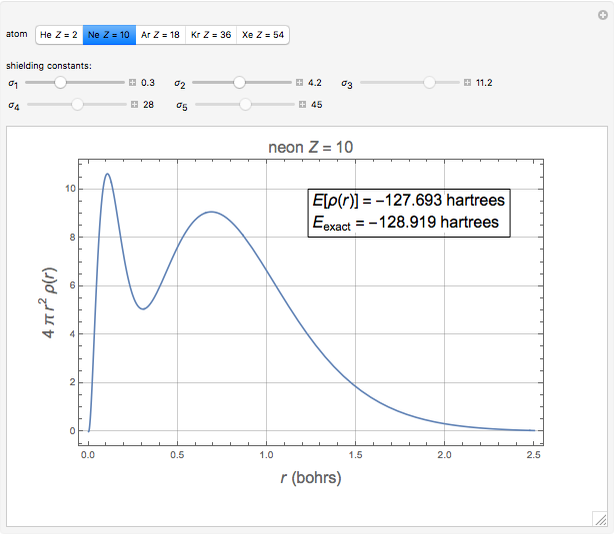
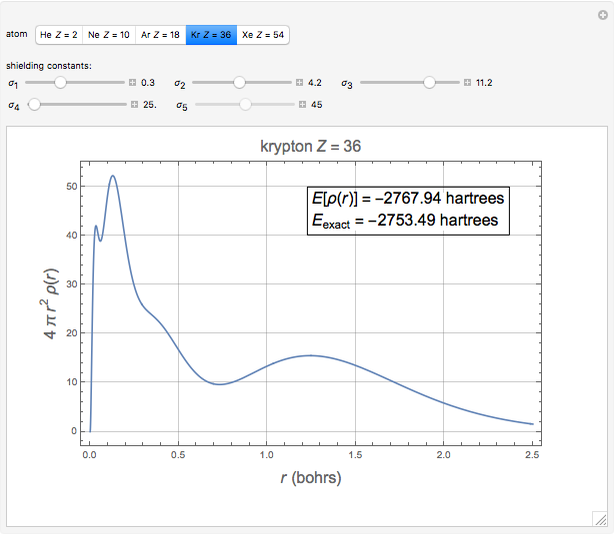
The total electron density is approximated by a sum of shells (one to five shells for He to Xe):

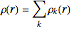, where ,

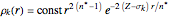which is suggested by Slater's rules for atomic orbitals.

The DFT functional takes the form

,

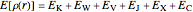with

,

, ,

,

,

, ,

.

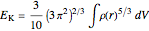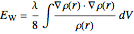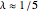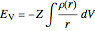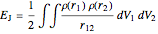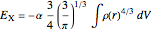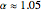The last formula is a conjecture by the author based on computations of atomic correlation energies.

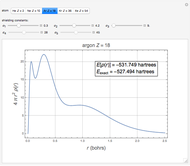
It is most convenient to carry out all the integrals numerically. The energy functional 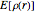, based on the selected shielding parameters 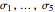, is computed and compared with the exact (nonrelativistic) energy of the atom. By the second Hohenberg–Kohn theorem, the optimized energy for the functional form of 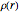is a minimum, although short of the exact energy.

References

[1] R. G. Parr and W. Yang, Density-Functional Theory of Atoms and Molecules, New York: Oxford University Press, 1989.

[2] J. Sun, J. W. Furness and Y. Zhang, "Density Functional Theory," Mathematical Physics in Theoretical Chemistry (S. M. Blinder and J. E. House, eds.), Amsterdam: Elsevier, 2018 Chapter 4. doi:10.1016/B978-0-12-813651-5.00004-8.

[3] W.-P. Wang and R. G. Parr, "Statistical Atomic Models with Piecewise Exponentially Decaying Electron Densities," Physical Review A, 16(3), 1977 pp. 891–902. doi:10.1103/PhysRevA.16.891.

[4] S. M. Blinder. "Shell Structure of Noble Gas Atoms" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/ShellStructureOfNobleGasAtoms.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send