Density of the Kou Jump Diffusion Process

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
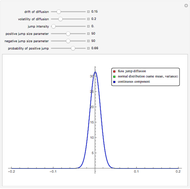
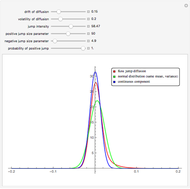
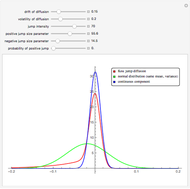
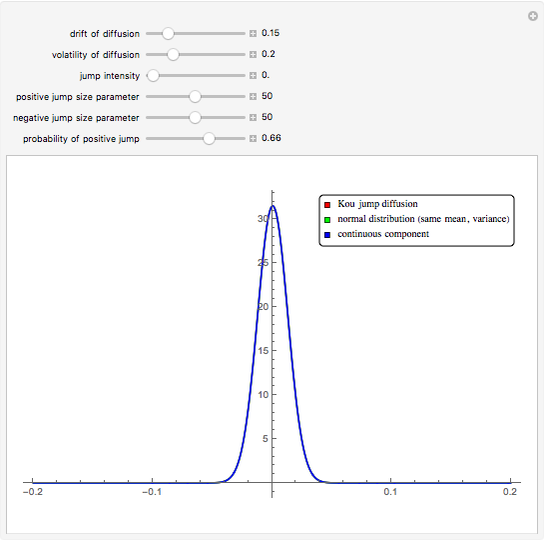
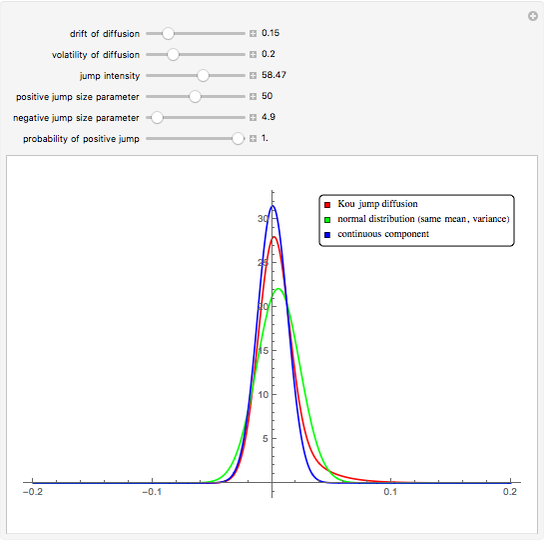
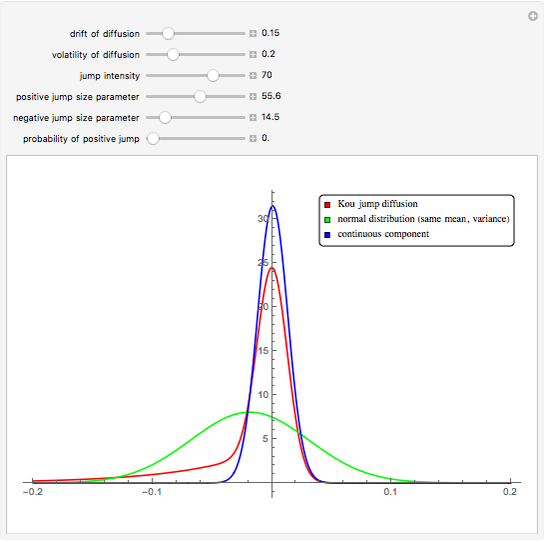
This Demonstration shows a graph of an approximate probability density function of the returns of the Kou jump diffusion process (red) together with the graphs of two closely related normal densities. The blue graph shows the density of the continuous component of the jump diffusion process. The green graph shows the density of the normal distribution with the same mean and standard deviation as the jump diffusion. When the jump intensity parameter is set to 0, all three curves coincide.
Contributed by: Andrzej Kozlowski (February 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Kou jump diffusion model is one of the most convenient improvements of the classical Black–Scholes model, in which a Lévy process (a jump process with independent increments) is used in place of the standard Wiener process. The Kou model is superior to the Black–Scholes model in fitting historical stock data while being more tractable than rival jump process models for the purpose of option pricing, since for several important types of options explicit formulas can be given for the option price in the Kou model but not in the others (this is due to the "memorylessness" property of the exponential distribution). Unfortunately there is no explicit formula for the probability density function of the Lévy process on which the Kou model is based. As with all Lévy processes, the distribution of values of the process at a given moment in time is infinitely divisible, but in this case it is not closed under convolution. This means that the distribution of returns depends on the time scale over which the data is sampled (i.e. the size of increment 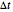 ). When
). When 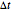 is small, an approximate formula for the probability density function can be obtained by means of the Taylor expansion. Here we take
is small, an approximate formula for the probability density function can be obtained by means of the Taylor expansion. Here we take 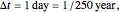 which is small enough for accurate approximation.
which is small enough for accurate approximation.
Reference
[1] S. Kou, "A Jump-Diffusion Model for Option Pricing," Management Science, 48, 2002 pp. 1086–1101.
Permanent Citation
"Density of the Kou Jump Diffusion Process"
http://demonstrations.wolfram.com/DensityOfTheKouJumpDiffusionProcess/
Wolfram Demonstrations Project
Published: February 25 2012