Rules from the book by M. Tribus are explored to deduce specified thermodynamic derivatives of the thermodynamical variables (energy  , enthalpy  , free energy of Helmholtz 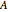 , free energy of Gibbs  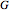, entropy  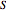, temperature  , pressure 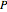 , and volume  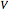) as functions of measurable quantities (temperature  , pressure 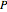 , volume  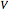, coefficient of thermal expansion  , coefficient of compressibility 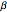 , heat capacity at constant pressure  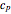, and heat capacity at constant volume  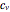). Sometimes the entropy  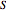will remain outside the derivatives.
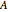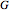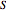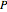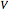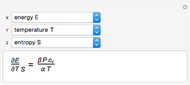
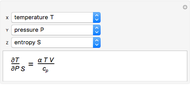
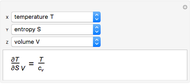
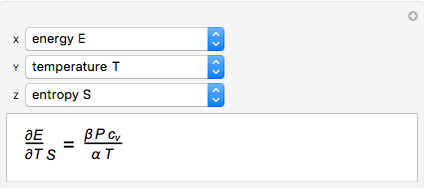
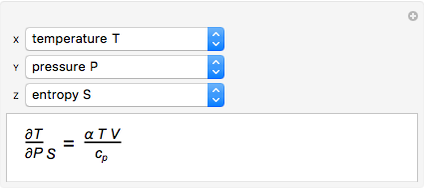
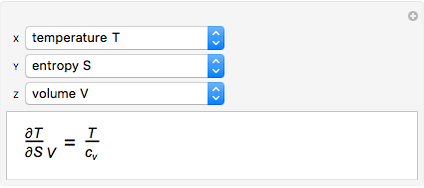
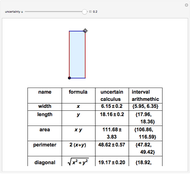
The main thermodynamical variables are energy  , enthalpy  , free energy of Helmholtz  , free energy of Gibbs  , entropy  , temperature  , pressure  , and volume  . It is possible to form 336 partial derivatives of the type 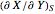 , where  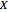,  , and 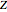 are among these eight variables. It is possible to express one derivative in terms of three outer derivatives. Among the 336 derivatives there are approximately 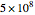 combinations, but only a small fraction of them have practical value. The Jacobian notation shows thermodynamic derivatives in an elegant manner. The application of Jacobians in thermodynamics appears to have started with Bryan [1]. A collection of Jacobian expressions is presented in [2] and [3]. Based on a suggestion made by E. Jaynes, Tribus developed rules for the deduction of thermodynamic partial derivatives [4]. For efficiency a new rule is added. [1] G. H. Bryan, (article title unknown), Encyklopedie der mathematishen Wissenschaften, Bd V, Teil 1, A. Sommerfeld, ed., Leipzig: G. B. Teubner, 1903 p. 113. [2] P. W. Bridgman, A Condensed Collection of Thermodynamic Formulas, Cambridge: Harvard University Press, 1925. [3] A. N. Shaw, "The Derivation of Thermodynamical Relations for a Simple System," Phil. Trans. Roy. Soc. A, 234(740), 1935 pp. 299–328. [4] M. Tribus, Thermostatics and Thermodynamics, Princton, NJ: Van Nostrand, 1961.
|
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_4.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_5.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_6.gif)
Embed Interactive Demonstration 
Browse all topics
