Deriving Hypergeometric Picard-Fuchs Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
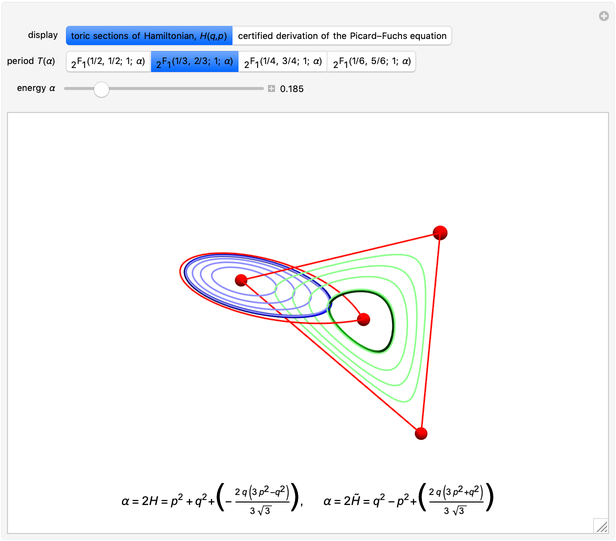
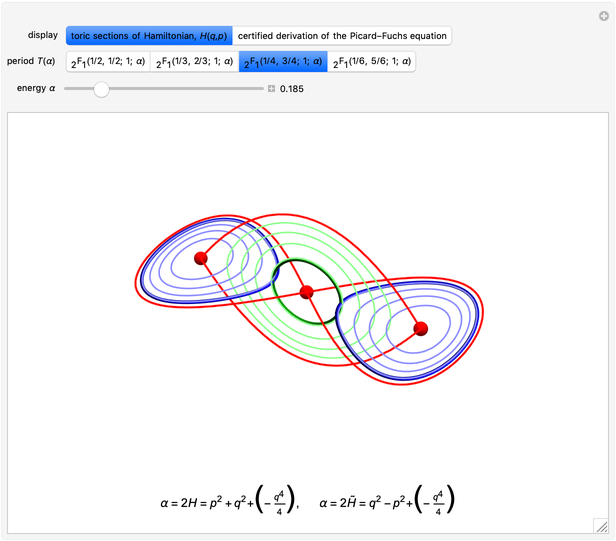
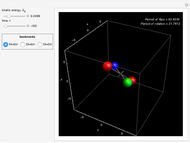
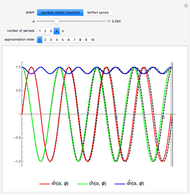
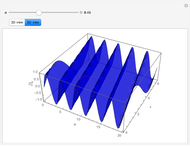
Applications of doubly periodic elliptic functions often require calculation of the dimensions of a period rectangle in the complex plane (see the Related Links). One approach follows from the fact that real and complex period-energy functions are also the solutions of a Picard–Fuchs equation [1]. This Demonstration gives four examples where a simple algebraic algorithm derives that the Picard–Fuchs equation can be written in a hypergeometric form (see Details). Solutions to this second-order ordinary differential equation are well-known in terms of the Gauss hypergeometric function 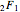 . Plotting cross sections of the toric energy surface allows us to depict energy inversion symmetry. The same symmetry permutes between real and complex periods.
. Plotting cross sections of the toric energy surface allows us to depict energy inversion symmetry. The same symmetry permutes between real and complex periods.
Contributed by: Brad Klee (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Our fast, certified algorithm PicardFuchs uses a recursive procedure adapted from another recent account [2]. We start our search by listing the  derivatives
derivatives
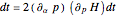 ,
,
 ,
,
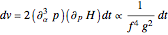 ,
,
and identifying functions 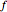 and
and  , which contribute divergences to integrands
, which contribute divergences to integrands 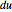 and
and  . The idea is to reduce the pole order of
. The idea is to reduce the pole order of 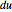 and
and  , removing all powers of
, removing all powers of 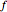 and
and  . In the source code, the function HermiteReduce accomplishes this task recursively and returns the reduced forms
. In the source code, the function HermiteReduce accomplishes this task recursively and returns the reduced forms
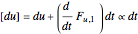 ,
,
 ,
,
 ,
,
where all 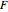 functions depend on variables
functions depend on variables 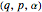 . Derivative calculations combine the chain rule and Hamilton's equations, while evaluating modulo
. Derivative calculations combine the chain rule and Hamilton's equations, while evaluating modulo  . The reduction algorithm divides nicely into separate subprocedures, which we certify by calculating null values.
. The reduction algorithm divides nicely into separate subprocedures, which we certify by calculating null values.
Once we know the reductions, it is easy to solve the linear system of equations on the  coefficients of
coefficients of
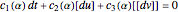 .
.
Exact differentials vanish in a complete integration over one cycle, finally leaving the Picard–Fuchs equation,
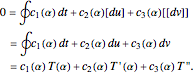
Each of these Picard–Fuchs equations can be written in the form
 ,
,
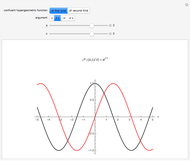
with signatures 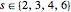 , as in the Ramanujan theory of elliptic functions [4, 5]. This differential equation is solved by
, as in the Ramanujan theory of elliptic functions [4, 5]. This differential equation is solved by
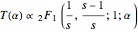 .
.
A second solution is obtained by energy inversion 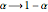 . Amazingly, the real period
. Amazingly, the real period 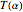 determines the complex period
determines the complex period 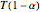 up to a rescaling of the time dimension. In general, this does not happen, as you might find by applying these algorithms to other Hamiltonian surfaces. This algorithm also leads to concise derivation of the Picard–Fuchs equation for a sextic double well [5, 6]. It will also produce certificates for A295870 and A300058 [7, 8].
up to a rescaling of the time dimension. In general, this does not happen, as you might find by applying these algorithms to other Hamiltonian surfaces. This algorithm also leads to concise derivation of the Picard–Fuchs equation for a sextic double well [5, 6]. It will also produce certificates for A295870 and A300058 [7, 8].
References
[1] M. Kontsevich and D. Zagier, "Periods," in Mathematics Unlimited: 2001 and Beyond (B. Engquist and W. Schmid, eds.), New York: Springer, 2001 pp. 771–808. www.maths.ed.ac.uk/~aar/papers/kontzagi.pdf.
[2] P. Lairez, "Computing Periods of Rational Integrals," Mathematics of Computation, 85, 2016 pp. 1719–1752. doi:10.1090/mcom/3054.
[3] B. C. Berndt, "Flowers Which We Cannot Yet See Growing in Ramanujan's Garden of Hypergeometric Series, Elliptic Functions, and q's," Special Functions 2000: Current Perspective and Future Directions (J. Bustoz, M. E. H. Ismail and S. K. Suslov, eds.), Dordrecht: Springer, 2001 pp. 61–85. doi:10.1007/978-94-010-0818-1_ 3.
[4] L. C. Shen, "On Three Differential Equations Associated with Chebyshev Polynomials of Degrees 3, 4 and 6," Acta Mathematica Sinica, 33(1), 2017 pp. 21–36. doi:10.1007/s10114-016-6180-1.
[5] M. Kreshchuk and T. Gulden. "The Picard–Fuchs Equation in Classical and Quantum Physics: Application to Higher-Order WKB Method." arxiv.org/abs/1803.07566.
[6] N. J. A. Sloane and B. Klee. The On-Line Encyclopedia of Integer Sequences. "G.f. satisfies: 120*(1-216*x)*A(x)+(1-3*(1-216*x)^2)*A'(x)-(1-216*x)*(2-216*x)*x*A''(x)=0, a(0)=1." oeis.org/A303790.
[7] N. J. A. Sloane and B. Klee. The On-Line Encyclopedia of Integer Sequences. "a(n) = binomial(3n,n)*CQC(n), where CQC(n) = A005721(n) = A005190(2n) is a central quadrinomial coefficient." oeis.org/A295870.
[8] N. J. A. Sloane and B. Klee. The On-Line Encyclopedia of Integer Sequences. "a(n) = binomial(3*n,n)/(2*Pi)*Integral_{x=0..2*Pi} (12*cos^2(x)*sin(x) + 20*sin^3(x))^(2*n) dx." oeis.org/A300058.
Permanent Citation