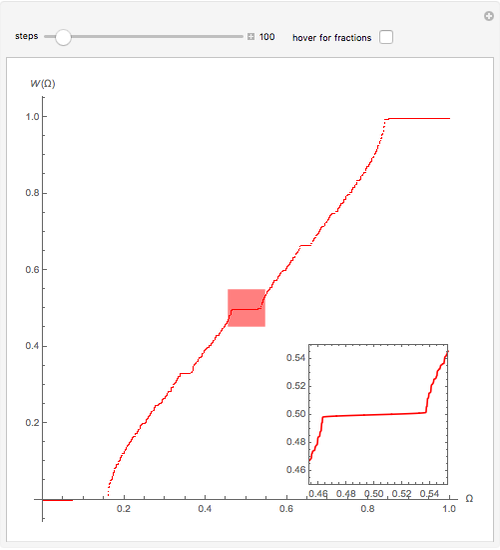
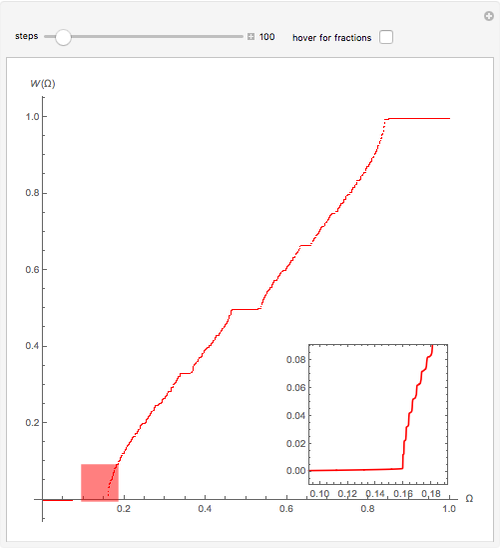
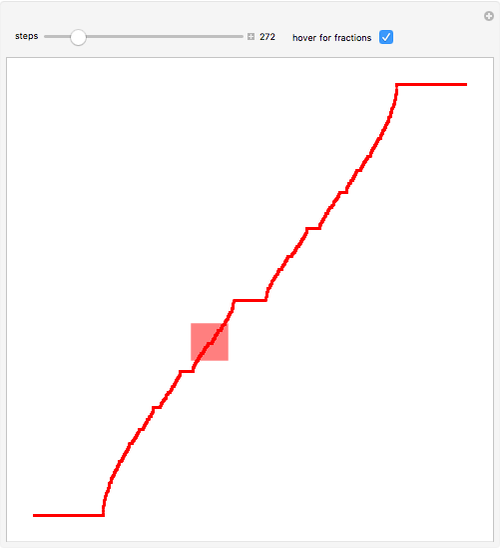
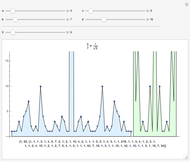
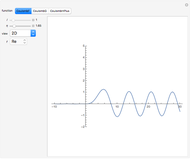
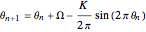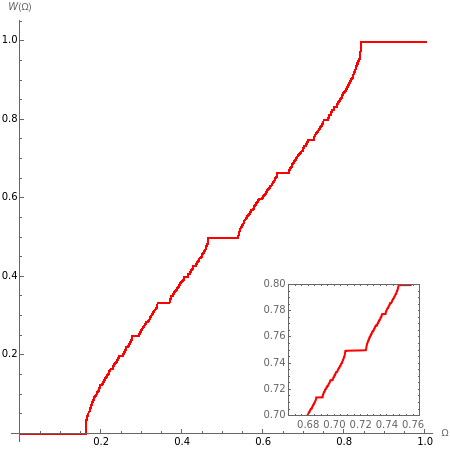
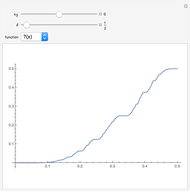
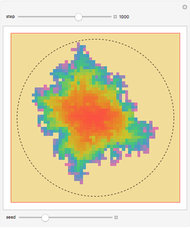
The mechanical system known as the kicked rotator yields a mapping named the circle map, given by , with . The motion is characterized by its winding number that represents an average frequency and is independent of the initial value of . The plot of this function is similar to a staircase whose steps appear at definite, ever-increasing rational values (use the hover version to see these fractions). After iterations, the value of differs precisely by from and the motion is periodic (mode locking). The points between steps are a Cantor set, where the function is discontinuous. The magnification on the bottom-right shows its self-similar structure.