Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

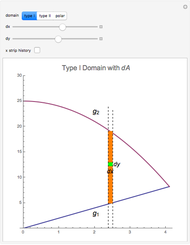
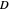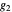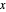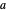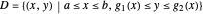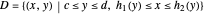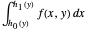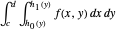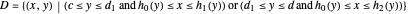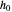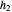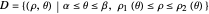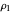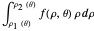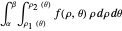Differential Element dA

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

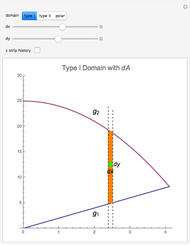
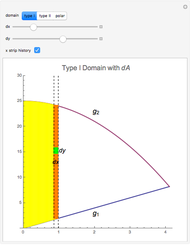
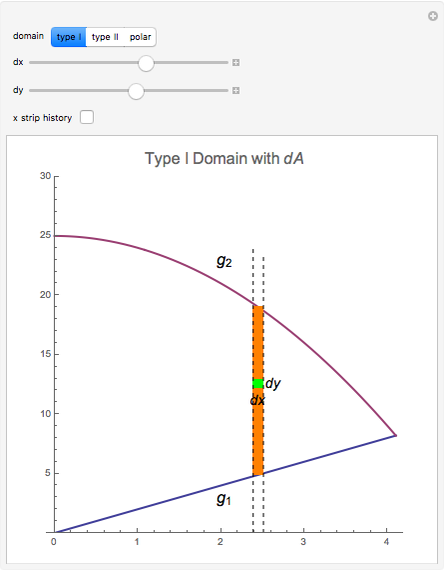
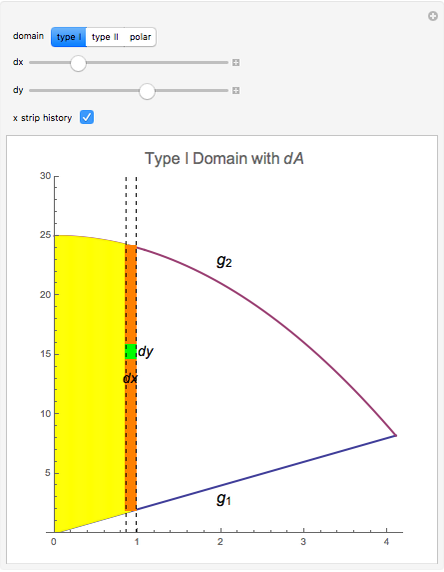
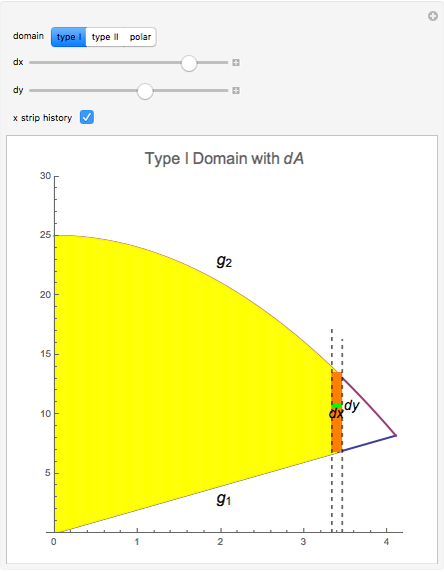
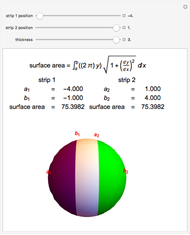
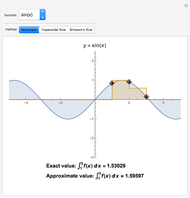
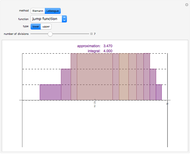
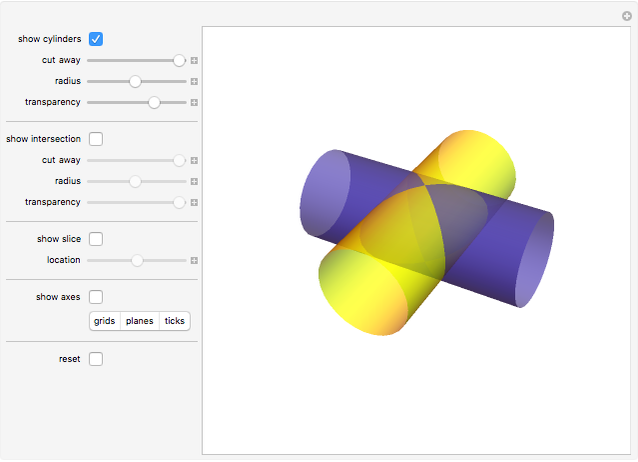
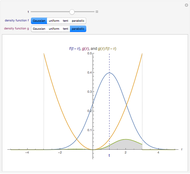
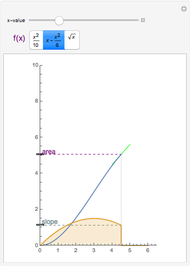
Integration over the region in the plane between the graphs of two continuous functions is performed by setting up type I or type II domains in Cartesian coordinates or as a polar domain in polar coordinates. Double integrals require a student to visualize the differential element of area covering the desired domain of integration. Using an integrand function of value 1 everywhere generates a double integral whose value is the area of the domain.

[more]

A plane region is type I if it lies between the graphs of two continuous functions and of on [, ], that is, . Vertical strips are integrated as shown by "x strip history" control.

A plane region is type II if it lies between the graphs of two continuous functions and of on [, ], that is, . Horizontal strips are integrated as shown by "y strip history" control.

When the domain consists of two type II domains as shown in the plot, a transition occurs from one domain to the other where the integral over the first domain is added to the integral over the second domain. , where , , and are continuous on [, ].

For a polar wedge the domain is defined by , where and are continuous on . Radial strips are integrated as shown by "wedge history" control.

[less]

Contributed by: Harry Bishop (April 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send