Diffusion and Reaction in a Catalyst Pellet

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
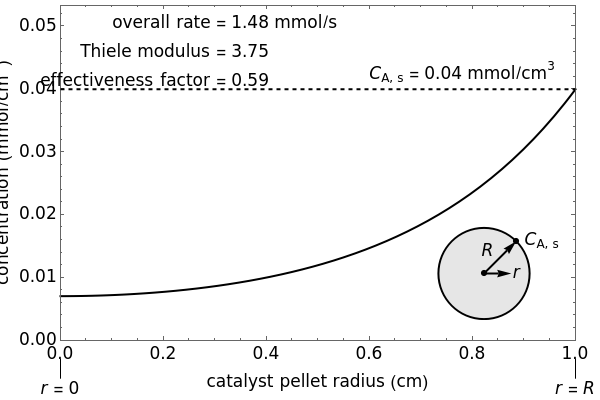
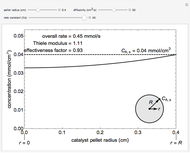
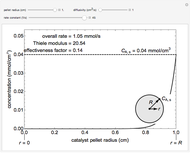
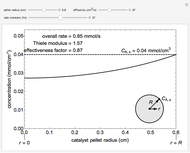
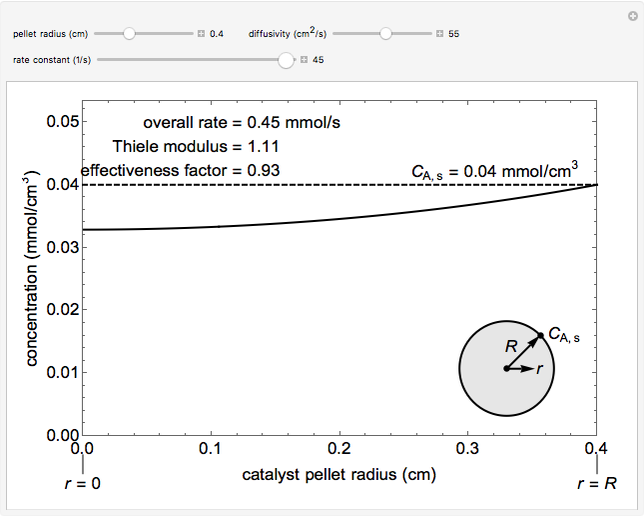
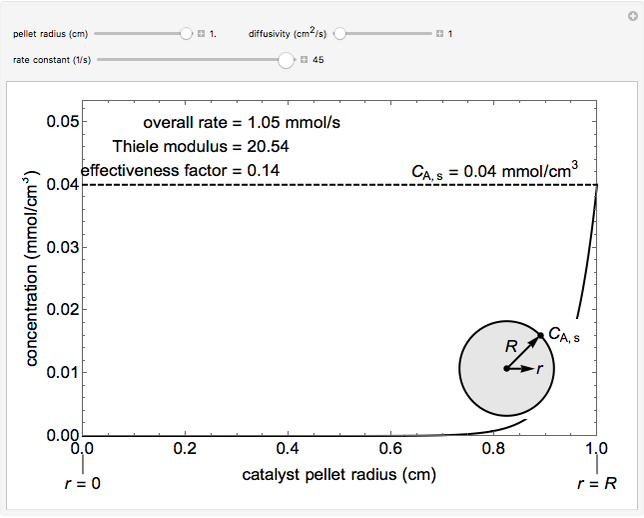
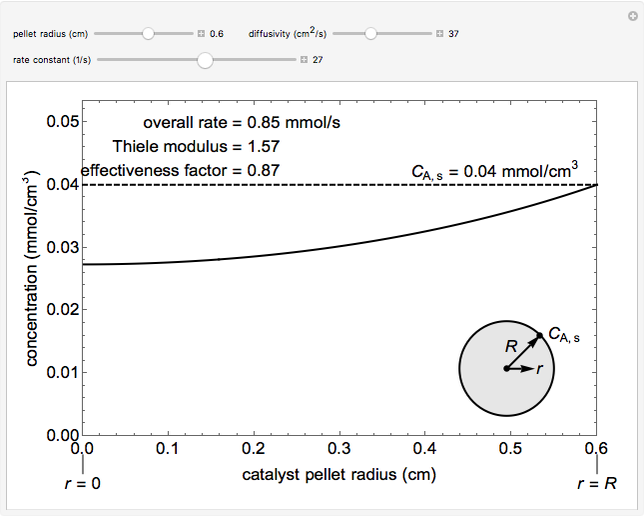
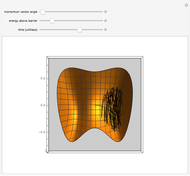
The overall rate of reaction in an isothermal, porous, spherical catalyst pellet is calculated for a first-order, gas-phase reaction that is limited by diffusion in the catalyst pores. This Demonstration plots the reactant concentration inside the catalyst pellet versus the pellet radius. Use the sliders to set the pellet radius, diffusivity and reaction rate constant. The Thiele modulus is a dimensionless number that represents the ratio of reaction rate to diffusion rate. The effectiveness factor is the overall rate of reaction divided by the rate of reaction if the entire catalyst were at 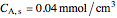 (the external surface concentration).
(the external surface concentration).
Contributed by: Rachael L. Baumann (October 2017)
Additional contributions by: John L. Falconer
(University of Colorado Boulder, Department of Chemical and Biological Engineering)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For the first-order reaction 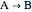 with rate law
with rate law 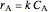 , the differential equation that describes diffusion and reaction in the catalyst pellet is:
, the differential equation that describes diffusion and reaction in the catalyst pellet is:
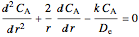 ,
,
where  is the radius of the catalyst pellet (
is the radius of the catalyst pellet (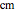 );
); 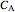 is the concentration in the catalyst (
is the concentration in the catalyst (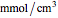 );
);  is the first-order rate constant (
is the first-order rate constant (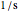 );
); 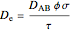 is the effective diffusivity (
is the effective diffusivity (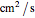 );
);  is the pellet porosity;
is the pellet porosity;  is the constriction factor;
is the constriction factor;  is tortuosity; and
is tortuosity; and  ,
,  and
and  are set based on typical values for these variables and are unitless.
are set based on typical values for these variables and are unitless.
The boundary conditions for the differential equation in spherical coordinates are:
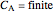 at
at 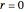 ,
,
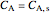 at
at 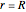 ,
,
where 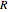 is the pellet radius (
is the pellet radius (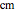 ) and
) and 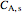 is the concentration (
is the concentration (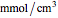 ) at
) at 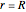 .
.
The differential equation in dimensionless form is:
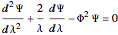 ,
,
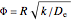 ,
,
where 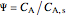 and
and 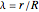 . The Thiele modulus
. The Thiele modulus 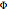 is the dimensionless ratio of the surface reaction rate to the diffusion rate.
is the dimensionless ratio of the surface reaction rate to the diffusion rate.
The boundary conditions in dimensionless form are:
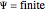 at
at  ,
,
 at
at 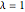 .
.
The solution to the differential equation in dimensionless form is:
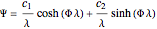 ,
,
where 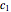 and
and 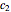 are constants that are obtained using the boundary conditions. The solution becomes:
are constants that are obtained using the boundary conditions. The solution becomes:
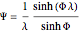 ,
,
and substituting the dimensionless variables into the solution yields:
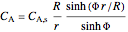 .
.
The overall rate of reaction 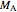 is:
is:
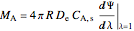 ,
,
where 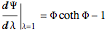 ,
,
substituting this into the solution yields:
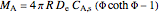 ,
,
where 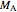 has units of
has units of 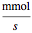 .
.
The effectiveness factor  is the reaction rate in the pellet divided by the reaction rate at the surface:
is the reaction rate in the pellet divided by the reaction rate at the surface:
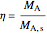 ,
,
where 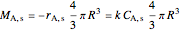 .
.
Thus,  is:
is:
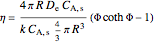 ,
,
which reduces to:
 .
.
Reference
[1] H. S. Fogler, Elements of Chemical Reaction Engineering, 4th ed., Upper Saddle River, NJ: Prentice Hall, 2006 pp. 813–852.
Permanent Citation