Digital Filters with Windowed Sinc Finite Impulse Response

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
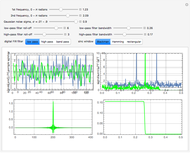
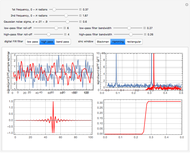
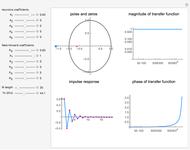
This Demonstration shows representations of windowed sinc low-pass, high-pass, and bandpass finite impulse response (FIR) digital filters. We display four windows changing simultaneously, in which one can choose three digital FIR filters by push-button control. These three filters can be selected along with their attendant slider control of roll-off and bandwidth characteristics. Using the first three sliders, one can generate two variable and summed frequency sine waves and added Gaussian noise with an adjustable standard deviation. Four additional slider bars control the roll-off and bandwidth characteristics of the filters. Three commonly used windows, the Blackman, Hamming and rectangular, can be selected for the sinc function with corresponding buttons. The time and frequency domain representation, as well as the kernel convolution shape, are displayed simultaneously with each filter's respective transfer response.
Contributed by: Dana Tremblay (February 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
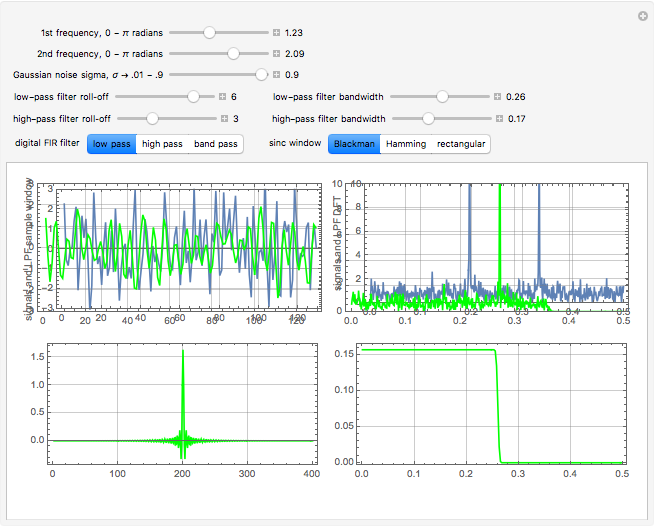
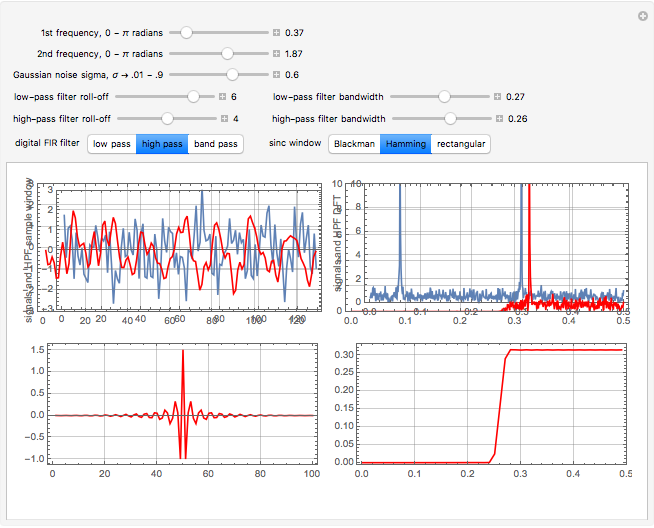
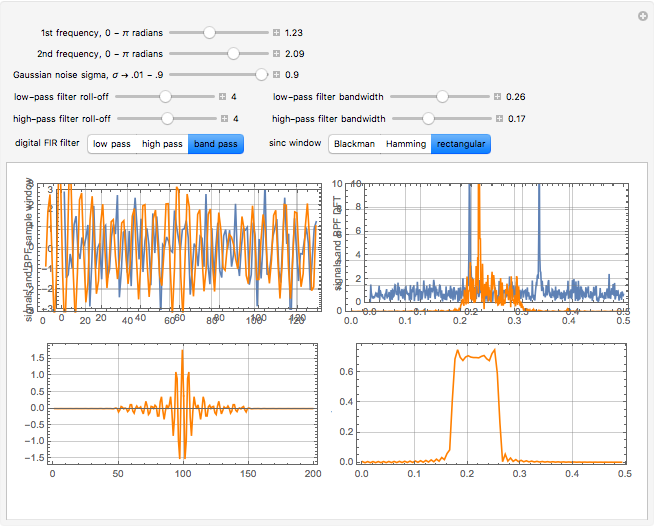
A raw data signal input buffer of sinusoidal input signals, with optional noise added, consists of 1024 samples in length for signal processing computation. However, for display clarity, 128 samples are chosen to present time-domain waveform detail. The input signals are in blue, each filter being push-button selectable. The filters are each color-coded and overlaid with that filter's outputs in green, red, and orange, which denote the low-pass, high-pass, and band-pass time domain output, respectively. A second window displays the corresponding frequency domain color-coded input and output result using a discrete Fourier transform (DFT) from 0 to  radians (i.e., Nyquist frequency or 0.5 Nyquist sampling rate) for each filter. A third window displays the shape of the selected filter's windowed sinc impulse response kernel used in the production of the filter's transfer function. FIR filters are based on the sum of the input data convolved, i.e.,
radians (i.e., Nyquist frequency or 0.5 Nyquist sampling rate) for each filter. A third window displays the shape of the selected filter's windowed sinc impulse response kernel used in the production of the filter's transfer function. FIR filters are based on the sum of the input data convolved, i.e., 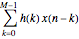 , using a basic impulse response transfer function kernel. The filter's response shape is shown to the right of the transfer function kernel in the fourth window. Finally, the effects of different window functions produced with the sinc function multiplied by typical Blackman, Hanning, and rectangular windows are shown as examples.
, using a basic impulse response transfer function kernel. The filter's response shape is shown to the right of the transfer function kernel in the fourth window. Finally, the effects of different window functions produced with the sinc function multiplied by typical Blackman, Hanning, and rectangular windows are shown as examples.
This Demonstration opens with all sliders to the far left and operates as follows:
1. Two sliders generate two independent sinusoids of adjustable frequency with  to
to  radians (0 to 0.5 Nyquist frequency). A concurrent windowed discrete Fourier transform (DFT) portrays their relative amplitude and frequency.
radians (0 to 0.5 Nyquist frequency). A concurrent windowed discrete Fourier transform (DFT) portrays their relative amplitude and frequency.
2. You can add more Gaussian noise with an adjustable standard deviation  using the third slider.
using the third slider.
3. You can select low-pass, high-pass, or band-pass windowed sinc convolution kernel ( ) multiplied with the selected window, which is generated with the roll-off characteristic. The low-pass response is the prototype to the high-pass response via "spectral inversion".
) multiplied with the selected window, which is generated with the roll-off characteristic. The low-pass response is the prototype to the high-pass response via "spectral inversion".
4. Two sliders control the low-pass band-pass response and two control the high-pass band-pass response. The band-pass response kernel is computed as the convolution of the low-pass and high-pass kernels.
Note the delay of the filters as well as the predicted stochastic increase of noise spectra in the pass bands as filter slopes increase. The first snapshot shows an asymetrical Blackman filter configuration, the second snapshot a Hamming window filter set and the third snapshot a Rectangular filter set.
References
[1] A. B. Openheim and R. W. Schafer, Digital Signal Processing, Englewood Cliffs, NJ: Prentice Hall, 1975.
[2] L. R. Rabiner and B. Gold, Theory and Application of Digital Signal Processing, Bell Telephone Laboratories and MIT Lincoln Laboratory, 1975.
[3] S. W. Smith, The Scientist and Engineer's Guide to Digital Signal Processing, Analog Devices, San Diego: California Technical Publishing, 1997.
[4] L. B. Jackson, Digital Filters and Signal Processing, Norwell, MA: Kluwer Academic Publishers, 1986.
[5] R. W. Hamming, Digital Filters, Englewood Cliffs, NJ: Prentice Hall, 1977.
[6] F. J. Taylor, Digital Filter Design Handbook, New York: Marcel Decker Inc., 1983.
[7] J. Lane, J. Datta, B. Karley, and J. Norwood, DSP Filters, Indianapolis, IN: Prompt Publications, 2001.
Permanent Citation