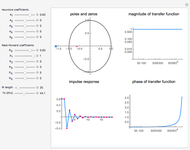
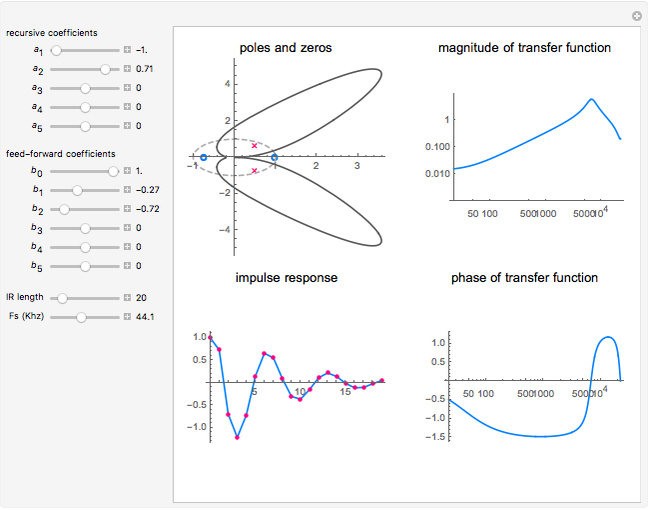
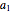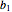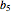Digital IIR Filter Design Showing Poles and Zeros

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
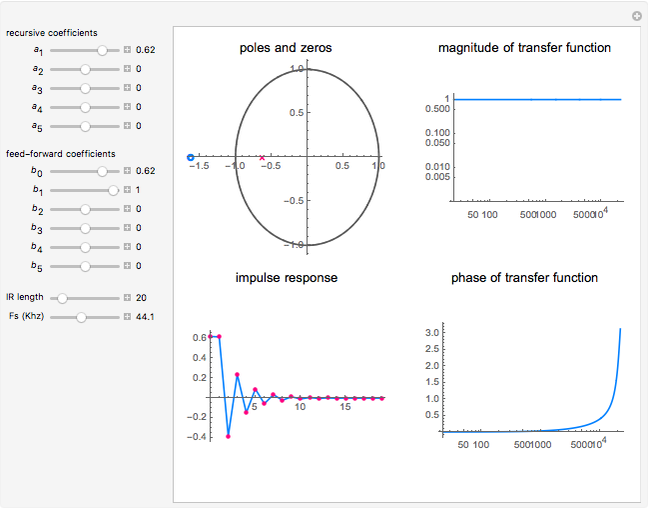
This Demonstration visualizes properties of a general fifth-order digital infinite impulse response (IIR) filter specified by the following expansion:
[more]
Contributed by: Hans Anderson (August 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
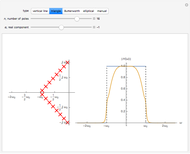
Snapshot 1: first-order all-pass filter
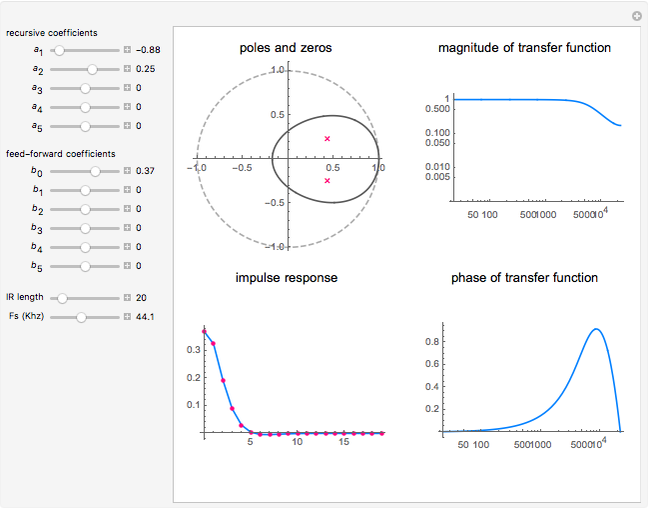
Snapshot 2: all-pole filter reducing amplitude of high frequencies
Snapshot 3: bandpass filter
The transfer function of the general fifth-order digital IIR filter as shown in this Demonstration is represented by
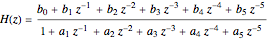 .
.
Given an input 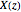 , the output of the filter,
, the output of the filter,  , is determined by
, is determined by  . Thus, the transfer function for the filter specifies the change in amplitude and phase on an input with frequency distribution defined by the unitary complex number
. Thus, the transfer function for the filter specifies the change in amplitude and phase on an input with frequency distribution defined by the unitary complex number  . For example, if the magnitude of the transfer function at frequency
. For example, if the magnitude of the transfer function at frequency  is 0.5, then the filter output amplitude at that frequency will be half the amplitude of the input.
is 0.5, then the filter output amplitude at that frequency will be half the amplitude of the input.
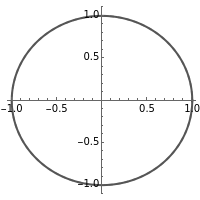
In filter design, it is helpful to know which complex valued inputs to the transfer function produce zero output amplitude and which inputs produce infinite output amplitude. This information is readily available by examining the numerator and denominator of the transfer function. Specifically, if for a given input value  the numerator is zero, then the entire transfer function evaluates to zero. Likewise, if for
the numerator is zero, then the entire transfer function evaluates to zero. Likewise, if for 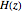 the denominator is zero, then the value of the transfer function is infinite. Complex values of
the denominator is zero, then the value of the transfer function is infinite. Complex values of  for which
for which 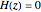 are called zeros of the transfer function, while values for which
are called zeros of the transfer function, while values for which 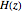 is infinite are called poles.
is infinite are called poles.
When we plot the transfer function of a digital filter, we let 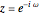 and generate the plot by varying
and generate the plot by varying  in the range
in the range 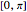 . In this way, we cover the entire range of frequencies from 0 up to the Nyquist frequency, which is half the sampling rate. Hence the value
. In this way, we cover the entire range of frequencies from 0 up to the Nyquist frequency, which is half the sampling rate. Hence the value 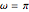 indicates the maximum frequency at which the filter operates without aliasing.
indicates the maximum frequency at which the filter operates without aliasing.
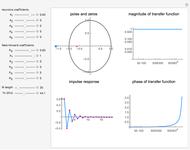
In this Demonstration, the poles and zeros plot shows the location of the poles and zeros in the complex plane. For a benchmark, the unit circle is also shown with a dashed line. The solid line shows the absolute value of the transfer function plotted in polar coordinates as the angle varies from  to
to  and from
and from  to
to 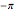 .
.
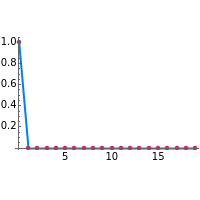
The impulse response plot shows the individual sample values that would result from applying the digital filter to an input containing a single one followed by zeros: 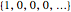 . This is useful for illustrating how the filter causes impulsive inputs to spread out in the time domain.
. This is useful for illustrating how the filter causes impulsive inputs to spread out in the time domain.
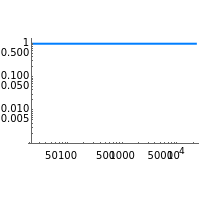
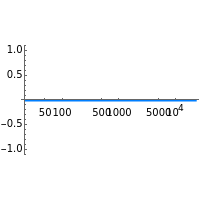
The magnitude and phase plots show 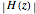 and
and 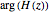 , respectively, plotted with
, respectively, plotted with 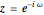 so that the frequency
so that the frequency  ranges from
ranges from  up to
up to  , which are the minimum and maximum frequencies representable in a digital system.
, which are the minimum and maximum frequencies representable in a digital system.
Reference
[1] R. Allred, Digital Filters for Everyone: Third Edition, Creative Arts & Sciences House, 2015.
Permanent Citation