Dijkstra's Algorithm
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
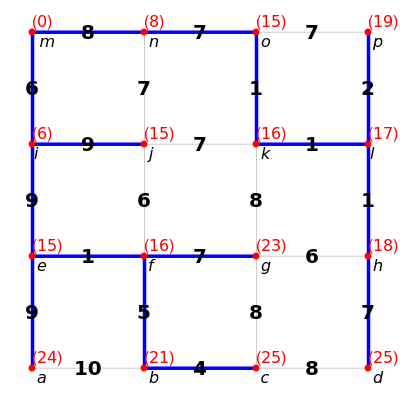
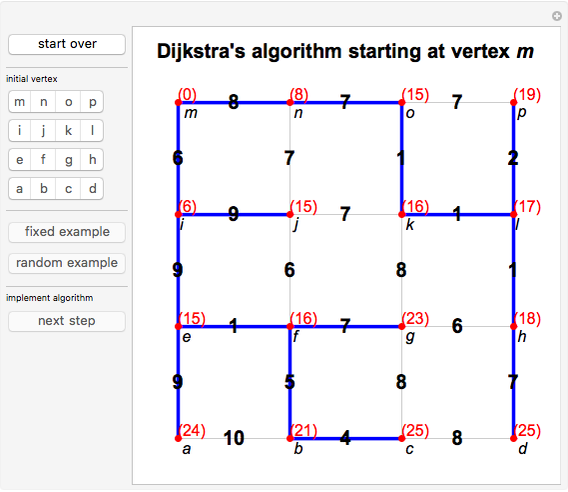
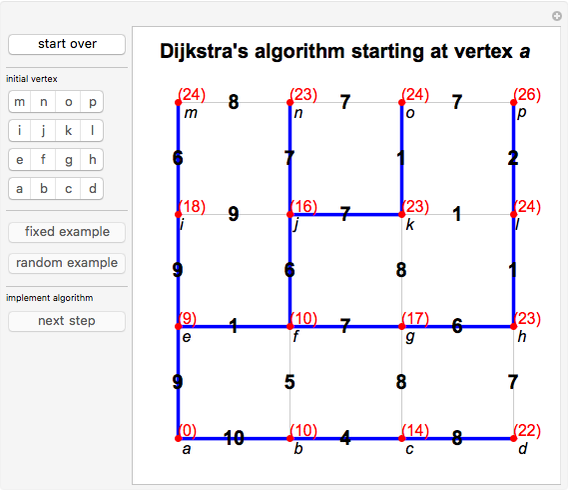
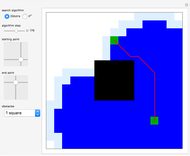
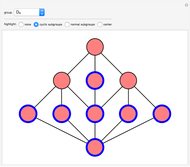
Dijkstra's algorithm finds the shortest-path spanning tree of a connected graph starting at a given vertex: the unique path in the tree from the starting vertex to any other vertex is the shortest path in the graph between those vertices. If you are interested only in the shortest path to a particular vertex, the algorithm can be stopped once that vertex is reached.
[more]
Contributed by: Marc Brodie (March 2011)
(Wheeling Jesuit University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation