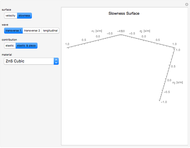
Directional Dependence of Acousto-Optic Figure of Merit

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
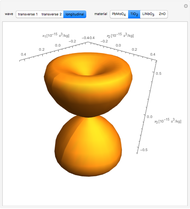
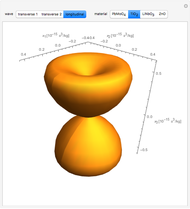
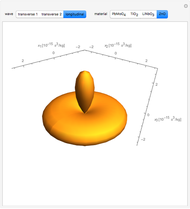
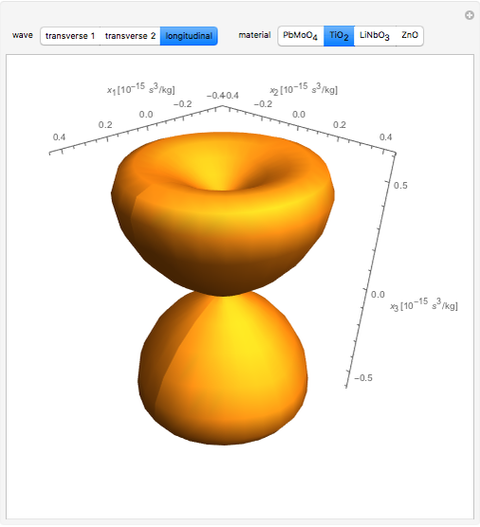
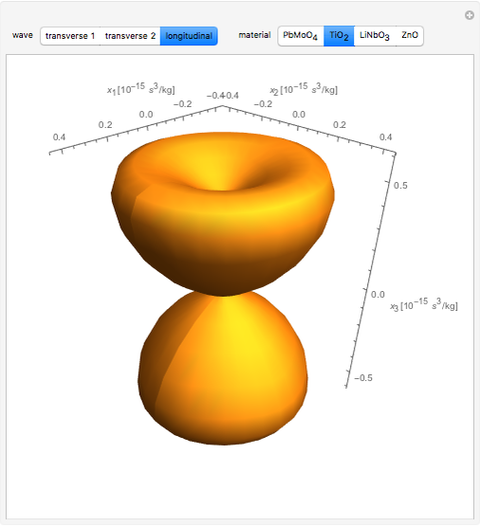
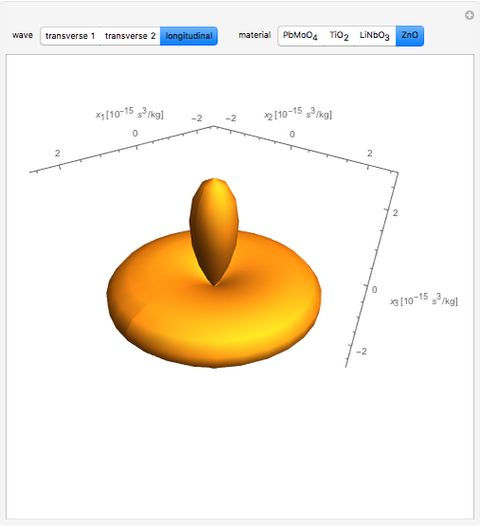
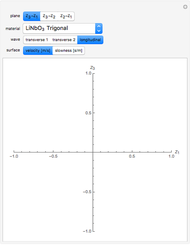
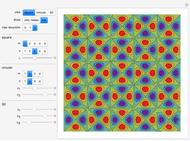
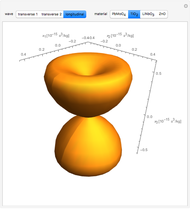
The acousto-optic figure of merit (FOM) indicates the ideal coupling orientation to maximize the refractive index change due to an acoustic signal.
[more]
Contributed by: Robert McIntosh (December 2013)
Open content licensed under CC BY-NC-SA
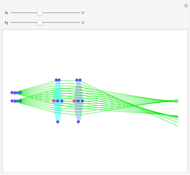
Snapshots
Details
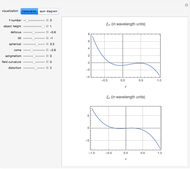
The figure of merit is calculated as 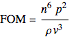 , where
, where  is the refractive index,
is the refractive index, 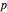 is the elastic constant,
is the elastic constant,  is the density, and
is the density, and  is the velocity. The velocity of sound in materials depends on the elastic constant
is the velocity. The velocity of sound in materials depends on the elastic constant  and the density, and is expressed as
and the density, and is expressed as 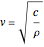 . Velocity calculations can often be very simple, but because of the anisotropy of many materials, the elastic constant
. Velocity calculations can often be very simple, but because of the anisotropy of many materials, the elastic constant  is actually a
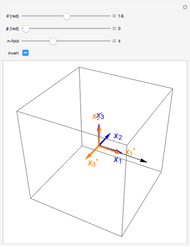
is actually a 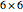 matrix of values. Solving for the velocity of the wave is done by using the Christoffel equation. This Demonstration also considers the contribution from the piezoelectric coupling. An excellent treatment of solving the Christoffel equation can be found in [2]. The directional dependent refractive index is calculated a bit differently. The
matrix of values. Solving for the velocity of the wave is done by using the Christoffel equation. This Demonstration also considers the contribution from the piezoelectric coupling. An excellent treatment of solving the Christoffel equation can be found in [2]. The directional dependent refractive index is calculated a bit differently. The 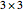 refractive index
refractive index  is transformed into
is transformed into 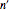 using the
using the 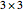 directional cosine
directional cosine  matrix,
matrix, 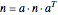 . The entry in the first row and first column of this matrix is the refractive index in the specified direction. The elasto-optic coefficient is calculated similarly, the only difference is the use of the
. The entry in the first row and first column of this matrix is the refractive index in the specified direction. The elasto-optic coefficient is calculated similarly, the only difference is the use of the 
 matrix
matrix 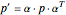 . By combining these calculations, the FOM can be determined in any direction. It is important to note that there are other types of acousto-optic FOM calculations—this one is perhaps the most common and indicates the best direction for a large diffraction of an incident optical signal. This calculation only considers the longitudinal elasto-optic effect, which considers an induced strain in an arbitrary direction that causes a refractive index change in the same direction.
. By combining these calculations, the FOM can be determined in any direction. It is important to note that there are other types of acousto-optic FOM calculations—this one is perhaps the most common and indicates the best direction for a large diffraction of an incident optical signal. This calculation only considers the longitudinal elasto-optic effect, which considers an induced strain in an arbitrary direction that causes a refractive index change in the same direction.
The coefficients used are from a variety of sources:
All of the elastic constants, density, and refractive index values are from [1].
The piezoelectric constants of 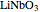 are from [2].
are from [2].
The permittivity of 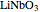 and ZnO are from [3].
and ZnO are from [3].
The elasto-optic coefficients of 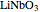 and
and 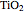 are from [2]; those of
are from [2]; those of  and ZnO are from [1].
and ZnO are from [1].
Further details can be found in [4].
References
[1] M. J. Weber, Handbook of Optical Materials, Boca Raton: CRC Press, 2002.
[2] R. E. Newnham, Properties of Materials: Anisotropy, Symmetry, Structure, Oxford, New York: Oxford University Press, 2005.
[3] Comsol Multiphysics. Material Library v4.3. (Dec 17, 2013) www.comsol.com/material-library.
[4] R. McIntosh, A. S. Bhalla, R. Guo, "Finite Element Modeling of Acousto-Optic Effect and Optimization of the Figure of Merit," Proceedings SPIE 8497, Photonic Fiber and Crystal Devices: Advances in Materials and Innovations in Device Applications VI, 849703, Oct 15, 2012. doi:10.1117/12.956441.
Permanent Citation