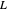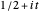Wolfram Demonstrations Project

Dirichlet

-functions are important in number theory. For example,

-functions are used to prove Dirichlet's theorem, which states that the arithmetic progression

(

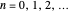) contains infinitely many primes, provided

and

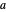are relatively prime. The zeros of

-functions can even be used to count how many primes less than

there are in arithmetic progressions.

This Demonstration graphs Dirichlet

-functions along the line

in the complex plane (the so-called "critical line"), and highlights the zeros that are encountered. Zeros occur where the real part (blue graph) and the imaginary part (red graph) are simultaneously 0.

Contributed by: Robert Baillie

Slider Zoom

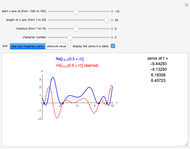
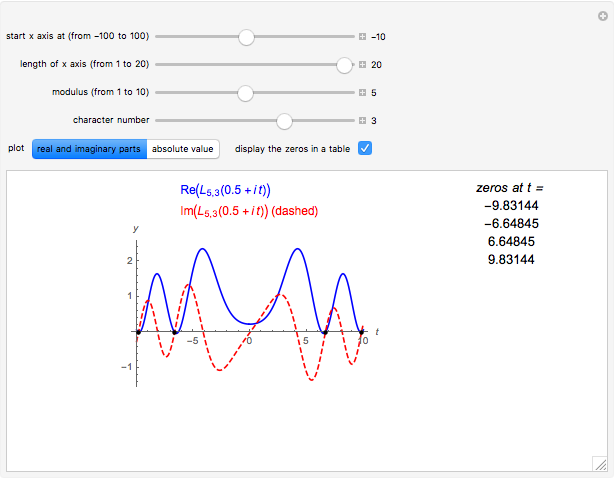
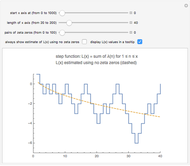
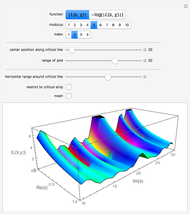
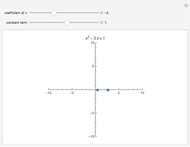
Snapshot 1: the graph of the Dirichlet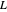

-function

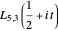for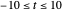

; the corresponding Dirichlet character

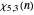has only real values, so the zeros of the

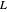-function occur in conjugate pairs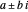

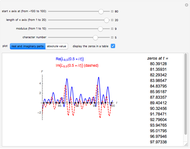
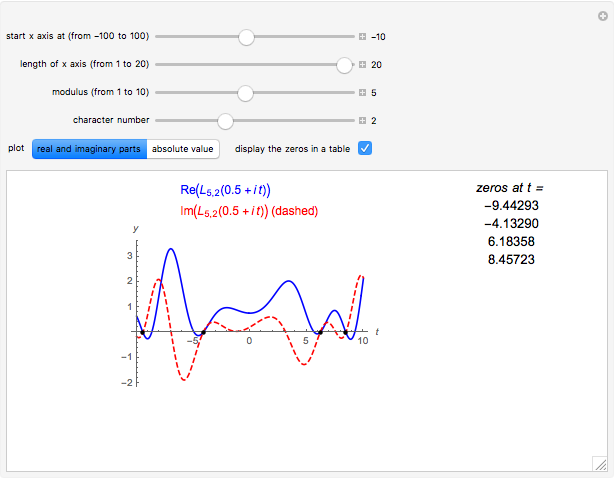
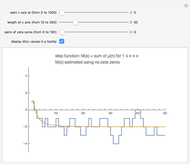
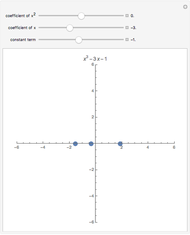
Snapshot 2: the graph of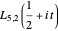

; the corresponding Dirichlet character

sometimes has complex values, so the zeros do not occur in conjugate pairs

Introduction:

Let

be a positive integer and suppose that

and

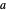are relatively prime (i.e.,

and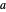

have no common factor greater than 1). Then Dirichlet's theorem says that the arithmetic progression

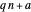has infinitely many primes. Dirichlet's theorem is proved in [1] by using Dirichlet characters and

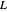-functions. The number of integers between 1 and

that are relatively prime to

is given by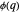

, where

is Euler's phi, the totient function.

For example, if

, then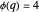

. There are four integers between 1 and 10 that are relatively prime to

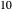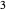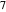, and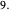

Therefore, each of the arithmetic progressions

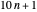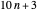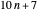, and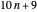

contains infinitely many primes, as

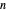takes the values

Dirichlet Characters and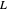

-functions:

Given a positive integer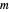

, a character function, usually denoted by

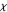(the Greek letter chi), is a function defined on the numbers mod

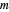such that, for all

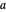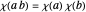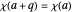and

, and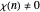

if and only if

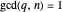. There are

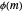different characters mod

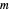. See reference [2] for more information.

For example, there are four characters mod 5. The third Dirichlet character mod 5 (in Mathematica's numbering system) has the following values at

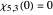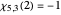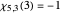, and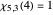

. The second character mod 5 takes complex values:

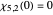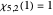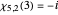, and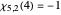

. (There are two other characters mod 5: the first is real; the fourth is complex.)

For any modulus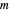

, there are at least two characters that take only real values, and usually some that take complex values.

The "Table of Dirichlet Characters" Demonstration (see the related link below) lets you choose the modulus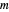

and see the values of all of the

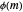different characters mod

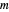For each character

, there is a corresponding Dirichlet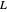

-function of the complex variable

, defined by

(1)

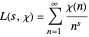In Mathematica notation, the Dirichlet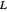

-function for the

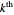character

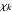mod

would be written as

(2)

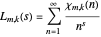These series converge if

. With analytic continuation, these functions can be extended to the entire complex plane (see [3]).

What do characters have to do with arithmetic progressions of the form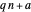

? This formula from page 252 of reference [1] illustrates the connection. If

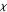is a character mod

, then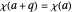

, so we can factor out

from the sum in equation (1) above to get

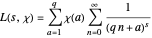This shows how arithmetic progressions arise naturally from expressions involving characters and

-functions.

Zeros of

-Functions:

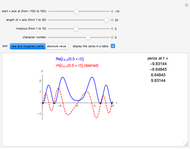
If a character is real (that is, if all its values are real), then the complex zeros of the corresponding Dirichlet

-function occur in conjugate pairs. That is, if

is a zero, then so is

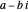. For example, we saw above that the third character mod 5 is real. The first two pairs of complex zeros for the corresponding Dirichlet

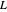-function

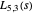are approximately

and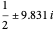

. These are the four complex zeros whose imaginary parts are closest to 0.

On the other hand, if the character is complex, then the zeros of the corresponding

-function are generally not in conjugate pairs. For example, consider the second character mod 5, which takes complex values. The four zeros of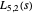

whose imaginary parts are closest to 0 are approximately

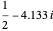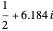, and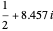

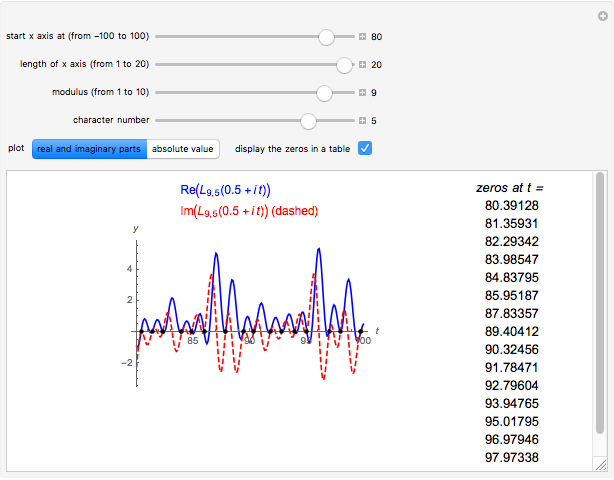
Dirichlet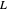

-functions

also have real zeros (so-called trivial zeros) at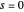

, and at either the negative even integers

, or at the negative odd integers

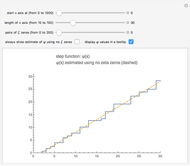
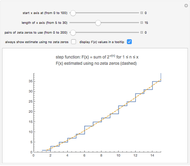
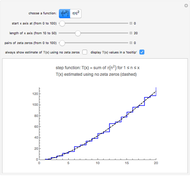
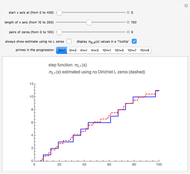
The Demonstration "A Formula for Primes in Arithmetic Progressions" (see the related link below) uses zeros of Dirichlet

-functions to count the primes less than or equal to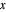

that are in various arithmetic progressions. Let

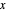be an integer. Estimate the primes in an arithmetic progression that are less than or equal to

, then estimate the number that are less than or equal to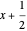

. If (after suitable rounding), these counts differ by 1, then

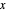must be prime!

The Generalized Riemann Hypothesis:

The generalized Riemann hypothesis (GRH) is the unproven conjecture that any complex (that is, a so-called nontrivial) zero of

whose real part is between 0 and 1, actually has real part equal to 1/2.

The GRH is a generalization of the more-famous Riemann hypothesis (RH), another unproven conjecture, that states that the complex zeros of the Riemann zeta function

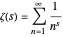
all have real part equal to 1/2. For these reasons, the vertical line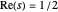

in the complex plane is called the "critical" line.

The Riemann zeta function is often used to prove theorems about primes, and to estimate the size of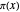

, the number of primes less than or equal to

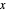In a somewhat analogous way,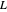

-functions are used to prove theorems, such as Dirichlet's theorem, about primes in arithmetic progressions, and to estimate how many primes there are in the arithmetic progression

that are less than or equal to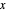

The RH and the GRH are among the most important unsolved problems in all of mathematics. They are important, among other reasons, because our current estimates of the number of primes less than or equal to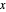

would become much more precise if the RH or the GRH could be proved.