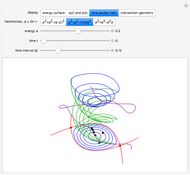
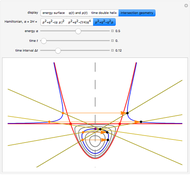
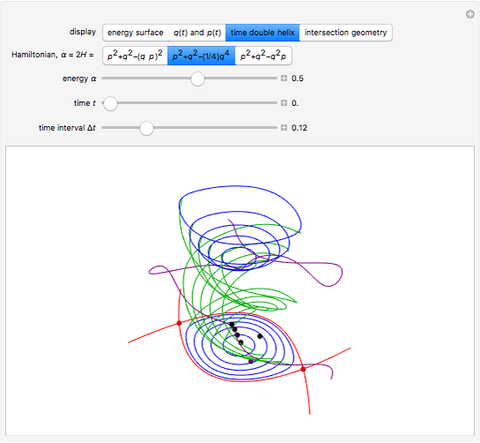
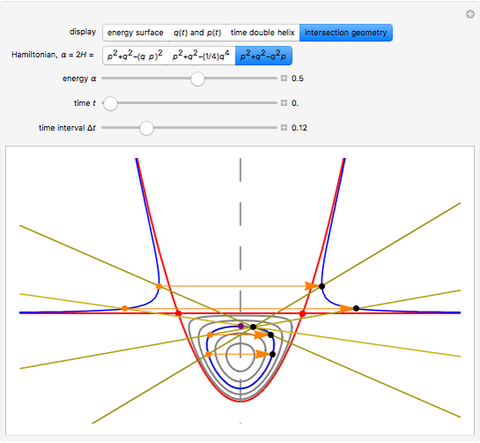
Discrete and Continuous Quartic Anharmonic Oscillation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
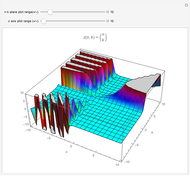
Using a birational transformation given by Harold Edwards (see Details), we apply the elliptic function  to solve time-dependence of anharmonic oscillation along the Hamiltonian surfaces
to solve time-dependence of anharmonic oscillation along the Hamiltonian surfaces 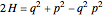 and
and 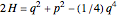 [1, 2]. After a shear symplectomorphism, the same solution also applies to the unusual cubic,
[1, 2]. After a shear symplectomorphism, the same solution also applies to the unusual cubic, 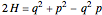 . Use this Demonstration to compare time evolution, point-to-point addition rules and intersection geometries.
. Use this Demonstration to compare time evolution, point-to-point addition rules and intersection geometries.
Contributed by: Brad Klee (April 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In the original article [1], two quartic families of elliptic curves,

and
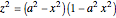
are related by the birational transformation
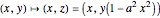 .
.
After additional changes of variables, we obtain the Hamiltonian forms
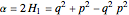 ,
,
 .
.
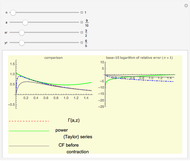
The elliptic function  accomplishes time parameterization of both surfaces. For the purposes of this Demonstration, a second-order approximation will certainly suffice,
accomplishes time parameterization of both surfaces. For the purposes of this Demonstration, a second-order approximation will certainly suffice,
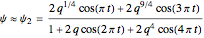 ,
,
with the nome 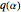 calculated by the Mathematica built-in function EllipticNomeQ.
calculated by the Mathematica built-in function EllipticNomeQ.
Solution of 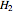 relative to
relative to 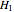 is guaranteed up to scale according to the pole-and-zero structure over
is guaranteed up to scale according to the pole-and-zero structure over  (Cf. [1], section 20). Comparison with the standard solution in terms of Jacobi elliptic functions verifies this assertion [3]. It is also possible to compare with numerical solutions to the equations of motion; however, discrete analysis makes for even better validation and deeper insight.
(Cf. [1], section 20). Comparison with the standard solution in terms of Jacobi elliptic functions verifies this assertion [3]. It is also possible to compare with numerical solutions to the equations of motion; however, discrete analysis makes for even better validation and deeper insight.
A third Hamiltonian surface is obtained by applying a quadratic shear,
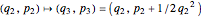 .
.
from quartic 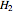 to cubic
to cubic 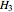 ,
,
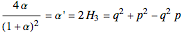 .
.
Generally, shear transformations are canonical or symplectic, both of which preserve Hamilton's equations of motion and leave time differentials 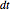 invariant. The Hamiltonian
invariant. The Hamiltonian 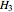 does not conform to the short Weierstrass equation associated with cubic anharmonic oscillation [4]. Nevertheless, a chord-and-tangent addition rule is easy to derive using a simple procedure [5, 6]. For chords, we obtain
does not conform to the short Weierstrass equation associated with cubic anharmonic oscillation [4]. Nevertheless, a chord-and-tangent addition rule is easy to derive using a simple procedure [5, 6]. For chords, we obtain
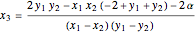 ,
,
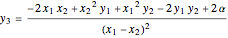 ,
,
and for tangents,
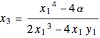 ,
,
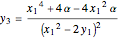 .
.
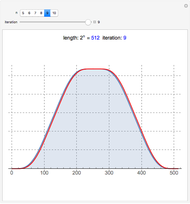
Sometimes we need to watch out for hidden points at infinity, but usually these equations are good enough to iterate along the time axis. Assume that point  generates an infinite sequence of unique points. We calculate
generates an infinite sequence of unique points. We calculate
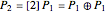
by tangent, and all subsequent

by chords. The iteration notation is consistent with cryptography literature [6]. Point iteration is not limited to the chord-and-tangent construction. Addition rules with hyperbolic and cubic intersection geometries exist for quartic surfaces 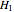 and
and 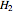 [7, 8]. These are unified rules, which avoid case splitting.
[7, 8]. These are unified rules, which avoid case splitting.
Iterating point addition along each Hamiltonian, we see linear action along the time axis. This is the property that Edwards refers to as a group homomorphism. Comparing 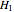 ,
, 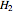 and
and 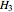 , we also see that iterations
, we also see that iterations 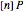 ,
, 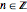 coincide only on the odd coset
coincide only on the odd coset 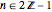 . These observations can be proven rigorously using only the built-in Mathematica function PolynomialReduce, as suggested by Hales [9]. Ultimately, we take the points sets
. These observations can be proven rigorously using only the built-in Mathematica function PolynomialReduce, as suggested by Hales [9]. Ultimately, we take the points sets 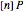 ,
, 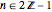 as discrete solutions along
as discrete solutions along 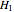 ,
, 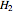 and
and 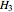 . Equivalence of discrete solutions immediately implies equivalence of continuous solutions, though only up to a rescaling of the period parallelogram,
. Equivalence of discrete solutions immediately implies equivalence of continuous solutions, though only up to a rescaling of the period parallelogram,
 .
.
The real periods 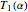 and
and 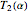 are also complete elliptic integrals
are also complete elliptic integrals
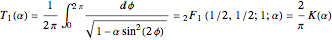 ,
,
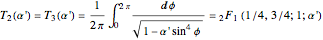 ,
,
taken along surfaces 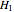 and
and 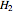 . Both integrals evaluate in terms of Gaussian hypergeometric function
. Both integrals evaluate in terms of Gaussian hypergeometric function 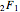 [10, 11].
[10, 11].
References
[1] H. M. Edwards, "A Normal Form for Elliptic Curves." Bulletin of the American Mathematical Society, 44, 2007 pp. 393–422. doi:10.1090/S0273-0979-07-01153-6.
[2] B. Klee. "Edwards's Solution of Pendulum Oscillation" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/EdwardssSolutionOfPendulumOscillation.
[3] W. P. Reinhardt and P. L. Walker, "Jacobian Elliptic Functions", NIST Digital Library of Mathematical Functions, Chapter 22. dlmf.nist.gov/22.
[4] B. Klee. "Weierstrass Solution of Cubic Anharmonic Oscillation" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/WeierstrassSolutionOfCubicAnharmonicOscillation.
[5] J. H. Silverman and J. T. Tate, Rational Points on Elliptic Curves, Cham: Springer, 2015. doi:10.1007/978-3-319-18588-0.
[6] C. Costello. "Pairings for Beginners." (Apr 4, 2018) craigcostello.com.au/pairing.
[7] C. Arene, T. Lange, M. Naehrig and C. Ritzenthaler. "Faster Computation of the Tate Pairing."arxiv.org/abs/0904.0854.
[8] D. J. Bernstein and T. Lange. "Explicit-Formulas Database." (Apr 4, 2018) hyperelliptic.org/EFD.
[9] T. Hales. "The Group Law for Edwards Curves." arxiv.org/abs/1610.05278.
[10] N. J. A. Sloane. The On-Line Encyclopedia of Integer Sequences. "a(n) = binomial(2n, n)^2." oeis.org/A002894.
[11] N. J. A. Sloane. The On-Line Encyclopedia of Integer Sequences. "a(n) = (4*n)! /((2*n)!*n!^2)." oeis.org/A000897.
Permanent Citation