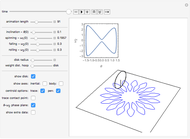
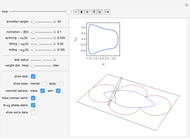
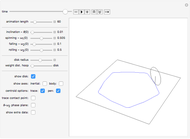
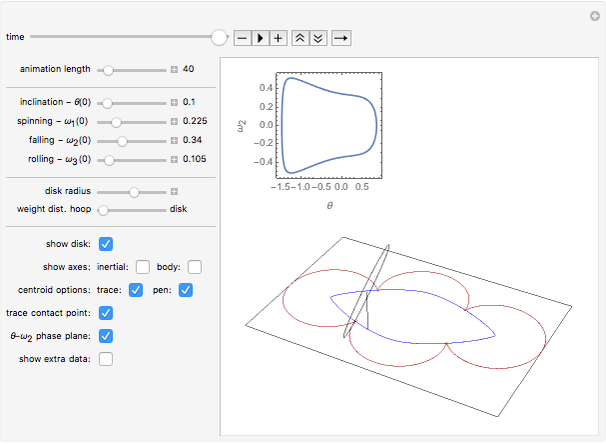
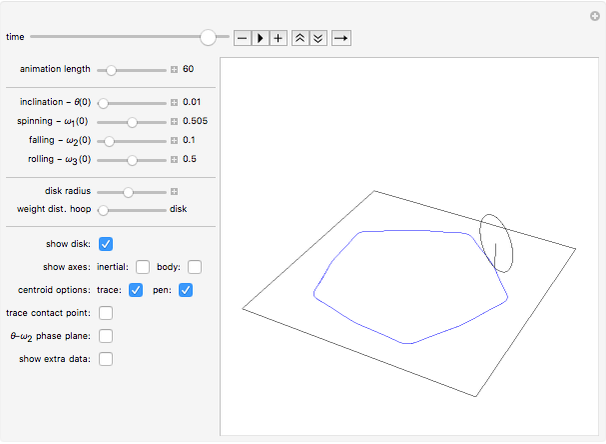
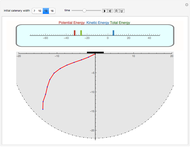
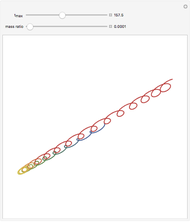
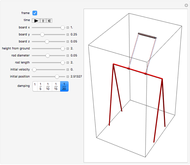
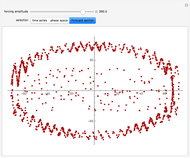
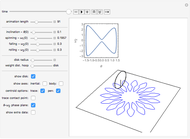
The rolling of a disk on a horizontal plane is a classic, integrable problem. This Demonstration allows you to manipulate the initial geometric and physical conditions to explore the solution space of the system. Some interesting solutions in which the centroid traces out figures approximating polygons have been bookmarked. Such solutions do not appear to have been previously discussed in the literature.
Although the stability analysis of the rolling disk is an old problem, there has been recent attention to both the classical non-dissipative dynamics and the physics of the late-stage motion, in particular the finite stopping time, using various models of dissipation. A reasonably complete list of references can be found in:
A. V. Borisov, I. S. Mamaev, and A. A. Kilin, "Dynamics of Rolling Disk," Regular and Chaotic Dynamics, 8(2), 2003 pp. 201–212.
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_4.gif)
Embed Interactive Demonstration 
Browse all topics
