Disks Centered on Vertices of Regular Polygons

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
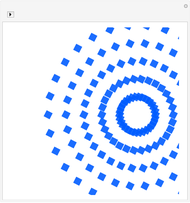
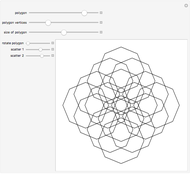
This Demonstration draws patterns constructed from colored disks whose centers are the vertices of an origin-centered regular polygon where you can vary the number of vertices  from 1 to 60. All vertex-centered disks have the same radius, so that each disk is tangent to both its neighbors and to an enclosing circle of unit radius and, for
from 1 to 60. All vertex-centered disks have the same radius, so that each disk is tangent to both its neighbors and to an enclosing circle of unit radius and, for 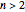 , to an origin-centered disk that is trapped by and tangent to the vertex-centered disks. You can vary the colors of the disks, the background, and the underlying polygon. The overall disk pattern may optionally be nested within the vertex-centered disks and/or the trapped origin-centered disk, zoomed in and out by a factor of from 1 to 3, rotated 360° in either direction, or colored by an automatic hue selection rule applied to a curved region taken from the Taoist symbol for yin and yang.
, to an origin-centered disk that is trapped by and tangent to the vertex-centered disks. You can vary the colors of the disks, the background, and the underlying polygon. The overall disk pattern may optionally be nested within the vertex-centered disks and/or the trapped origin-centered disk, zoomed in and out by a factor of from 1 to 3, rotated 360° in either direction, or colored by an automatic hue selection rule applied to a curved region taken from the Taoist symbol for yin and yang.
Contributed by: Mark D. Normand (June 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
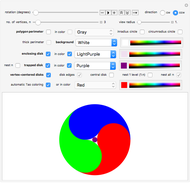
Snapshot 1: Disks centered on the three vertices of an equilateral triangle colored using the hue selection rule and modified disk shape of the "automatic Tao coloring" option, with the comma-shaped regions pointing in the counterclockwise direction.
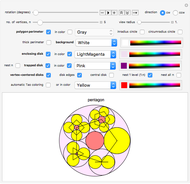
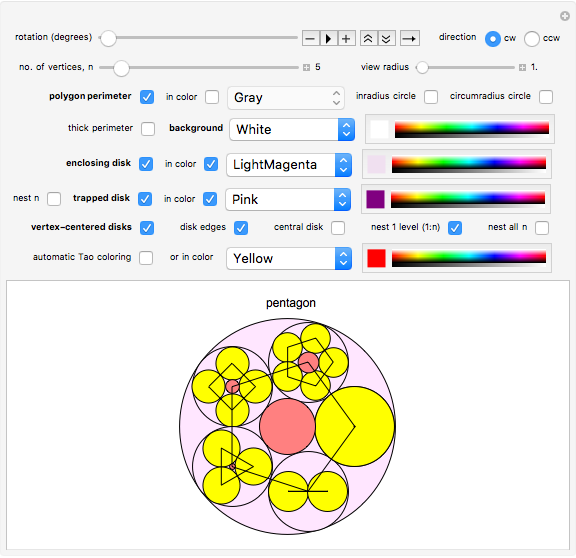
Snapshot 2: Disks centered on the five vertices of a regular pentagon shown with smaller nested polygon-centered disks whose number of vertices increases in clockwise order and whose edges are emphasized.
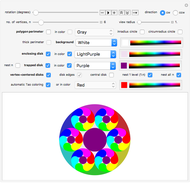
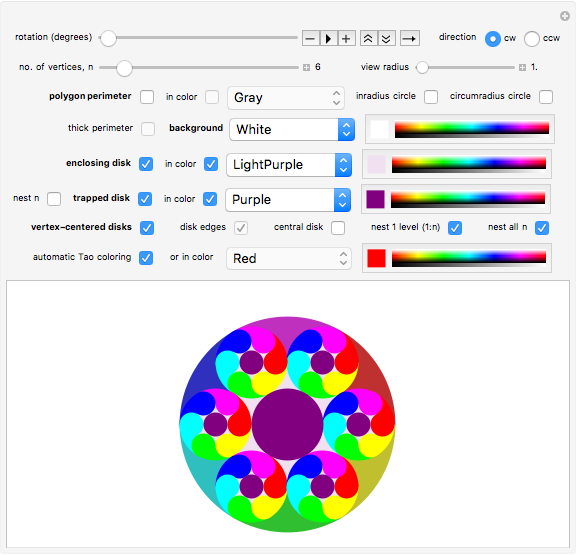
Snapshot 3: Disks centered on the six vertices of a hexagon shown with smaller nested hexagon-centered disks colored using the "automatic Tao coloring" option.
Snapshot 4: Disks centered on the seven vertices of a regular heptagon shown with smaller nested polygon-centered disks whose number of vertices increases in counterclockwise order, colored using the "automatic Tao coloring" option and containing central disks drawn in colors complementary to the surrounding disks.
Snapshot 5: A regular octagon shown with smaller polygons having from one to eight vertices located at each vertex, increasing in clockwise order and showing a smaller octagon located within the larger one.
Snapshot 6: Disks centered on the 12 vertices of a regular dodecagon shown with smaller nested dodecagon-centered disks and a nested trapped center disk. All disks are drawn with unemphasized edges and with central disks drawn in colors complementary to the surrounding disks.
A regular polygon having  vertices (
vertices (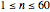 ) may be drawn centered on the origin where
) may be drawn centered on the origin where  is chosen with a slider. A disk centered on each polygon's vertex may be drawn with radius
is chosen with a slider. A disk centered on each polygon's vertex may be drawn with radius 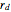 such that the disk is tangent to each of the two neighboring disks and also to an enclosing disk whose radius
such that the disk is tangent to each of the two neighboring disks and also to an enclosing disk whose radius  . For
. For 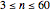 , an origin-centered disk may be drawn that is trapped by and tangent to the
, an origin-centered disk may be drawn that is trapped by and tangent to the  vertex-centered disks and has radius
vertex-centered disks and has radius 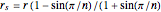 . If
. If  then
then 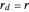 ; otherwise,
; otherwise,  .
.
The coordinates of the  vertices of an
vertices of an  -sided regular polygon are at (
-sided regular polygon are at (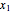 ,
, 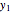 ) through (
) through (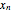 ,
, 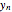 ). The
). The 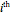 vertex of the regular polygon is located at angle
vertex of the regular polygon is located at angle  radians from the standard unit circle's angular origin at the three o'clock position, where the angular increment
radians from the standard unit circle's angular origin at the three o'clock position, where the angular increment 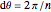 . The length
. The length  of each polygon side is
of each polygon side is 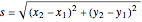 . The radius
. The radius 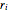 of a circle inscribed within the regular polygon (the "inradius") is
of a circle inscribed within the regular polygon (the "inradius") is 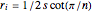 . The radius
. The radius 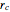 of a circle circumscribed about the regular polygon (the "circumradius") is
of a circle circumscribed about the regular polygon (the "circumradius") is 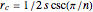 .
.
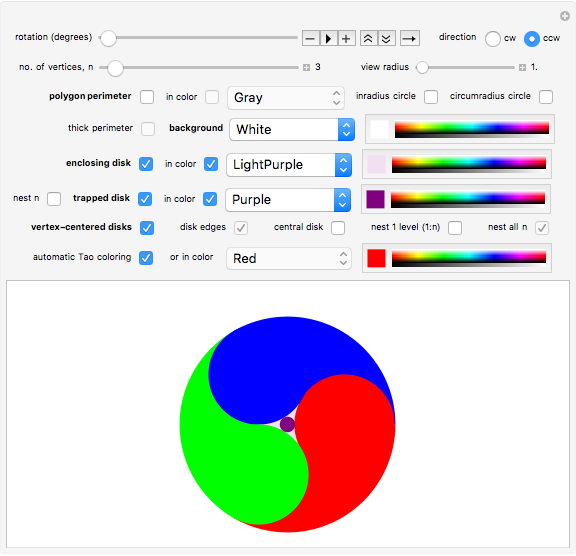
The "rotation (degrees)" slider allows manual rotation of the whole image and is followed by controls that also allow it to be run as an animation. The two "direction" radio buttons (clockwise and counterclockwise) control three different circular directions: (1) the rotation direction of the whole image that is controlled by the "rotation (degrees)" slider; (2) the direction in increasing number of vertices of the vertex-centered disks when both the "nest 1 level (1:n)" box is checked and the "nest all n" box is unchecked; and (3) the direction from the thin to the thick end of the comma-shaped colored regions shown when the "automatic Tao coloring" box is checked. The "view radius" slider allows zooming in and out from the image by a factor of from 1 to 3.
The color of the five items labeled in bold (polygon perimeter, background, enclosing disk, trapped disk and vertex-centered disks) may be selected from the popup menus to their right, which list all 24 Mathematica system colors. Four of the five menus also have a 25th item, "you choose ->", which when chosen allows any RGB color to be selected using the color slider to its right. The color of the  "vertex-centered disks" may be specified using either the "automatic Tao coloring" checkbox or the popup menu and color slider controls to its right.
"vertex-centered disks" may be specified using either the "automatic Tao coloring" checkbox or the popup menu and color slider controls to its right.
The "automatic Tao coloring" checkbox colors the vertex-centered disks and the enclosing disk based on the two-part Taoist symbol for yin and yang. In that symbol, each of the two disks centered on the endpoints of a line segment (digon) whose length equals the diameter of either disk is colored the same as one of the two background regions from the enclosing disk. This forms two adjacent comma-shaped regions.
The entire circular image pattern is replicated within each vertex-centered disk if the "nest 1 level (1:n)" box is checked. In that case the "no. of vertices, n" slider is also limited to a maximum value of 12. The pattern of disks centered on an  -gon is repeatedly nested in all
-gon is repeatedly nested in all  vertex-centered disks if the "nest all n " box is checked. Otherwise, the pattern of disks nested on the
vertex-centered disks if the "nest all n " box is checked. Otherwise, the pattern of disks nested on the  disk contains
disk contains  vertex-centered disks. When the "central disk" box is checked, a central disk in the complementary color of the surrounding disk and having 1/6 its diameter is drawn. When the "disk edges" box is checked, the edges of all disks are emphasized. When the "automatic Tao coloring" box is checked, all disks are drawn with their edges unemphasized. When the "nest n" box is checked, the entire circular image pattern is replicated within the center disk that is trapped by the
vertex-centered disks. When the "central disk" box is checked, a central disk in the complementary color of the surrounding disk and having 1/6 its diameter is drawn. When the "disk edges" box is checked, the edges of all disks are emphasized. When the "automatic Tao coloring" box is checked, all disks are drawn with their edges unemphasized. When the "nest n" box is checked, the entire circular image pattern is replicated within the center disk that is trapped by the  surrounding vertex-centered disks.
surrounding vertex-centered disks.
Permanent Citation