Dissection of Hill's Tetrahedron of Type 1
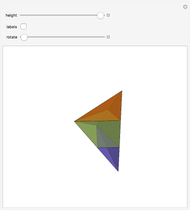
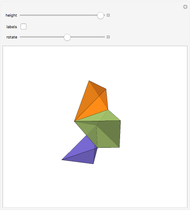
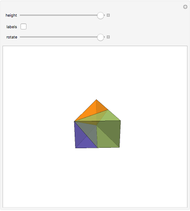
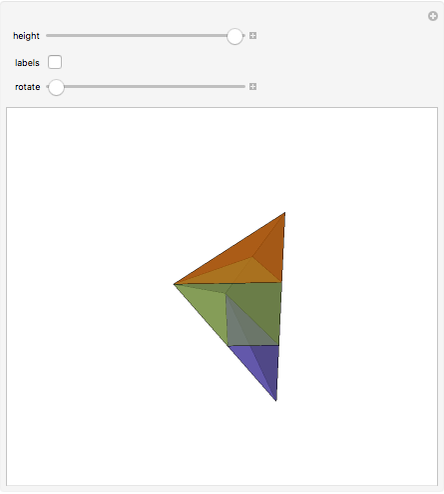
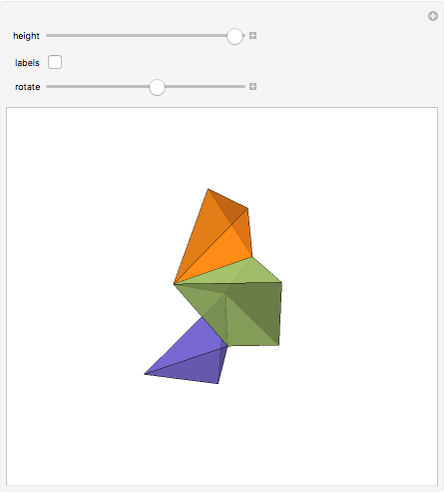
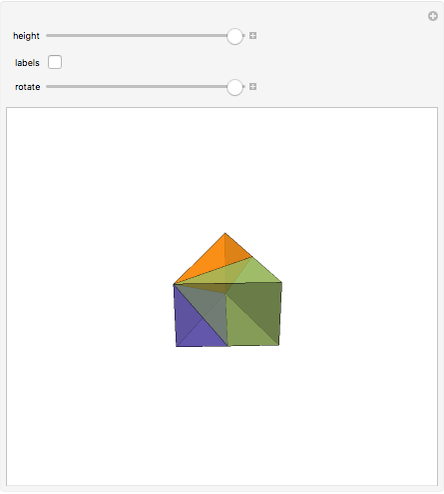
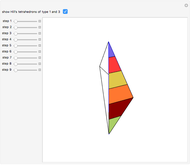
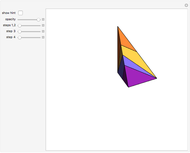
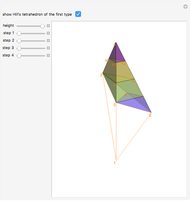
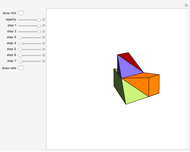
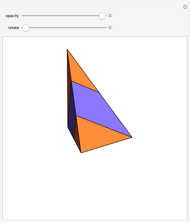
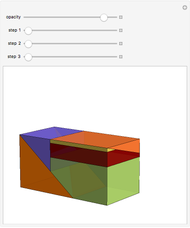
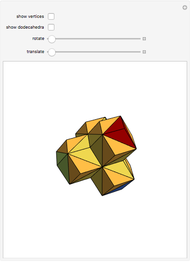
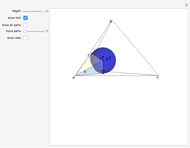
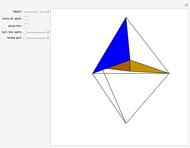
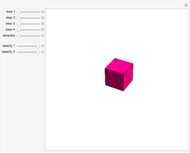
This Demonstration gives a three-piece dissection of the general Hill's tetrahedron of type 1 into a triangular prism.
Contributed by:
Izidor Hafner
X
X
X
Show Source Code
|
Download Source Code Notebook
Show Initialization Code
The dissection was discovered by P. Schöbi (1985) and independently by A. Hanegraaf.
G. N. Frederickson,
Dissections: Plane & Fancy
, Cambridge University Press, 2002 pp. 234–235.
Dissection
(
Wolfram
MathWorld
)
Tetrahedron
(
Wolfram
MathWorld
)
Three-Piece Dissection of a Hill Tetrahedron into a Triangular Prism
(
The Wolfram Demonstrations Project
)
"
Dissection of Hill's Tetrahedron of Type 1
" from
The Wolfram Demonstrations Project
http://demonstrations.wolfram.com/DissectionOfHillsTetrahedronOfType1/
Contributed by:
Izidor Hafner
3D Graphics
Polyhedra
Recreational Mathematics
Solid Geometry
Six-Piece Dissection of Hill's Tetrahedron of Type 3 into a Triangular Prism
Four-Piece Dissection of Juel's Pyramid to a Prism
Four-Piece Dissection of Hill's Tetrahedron of Type 2 into a Triangular Prism
Three-Piece Dissection of a Hill Tetrahedron into a Triangular Prism
Sydler's Dissection of a Hill Tetrahedron into an Isosceles Triangular Prism
Hanegraaf's Rectangular Block of Size 2 to a Cube Dissection
Six-Piece Dissection of a Tetrahedron into Its Mirror Image
Gerling's 12-Piece Dissection of an Irregular Tetrahedron into Its Mirror Image
Definitions of Hill's Tetrahedra
Decomposition of the Tetrahedron into Four Congruent Symmetrical Parts
Make a new version of this Demonstration
Upload a new Demonstration
Contact The Wolfram Demonstrations Project Team
Site Index
Wolfram Research
© 2008
The Wolfram Demonstrations Project & Contributors
Terms of Use
Privacy Policy
RSS
Atom
