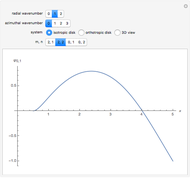
Distribution of End-to-End Distances in Linear Substituted Polymethylenes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
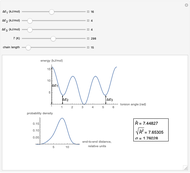
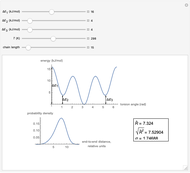
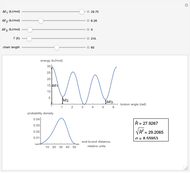
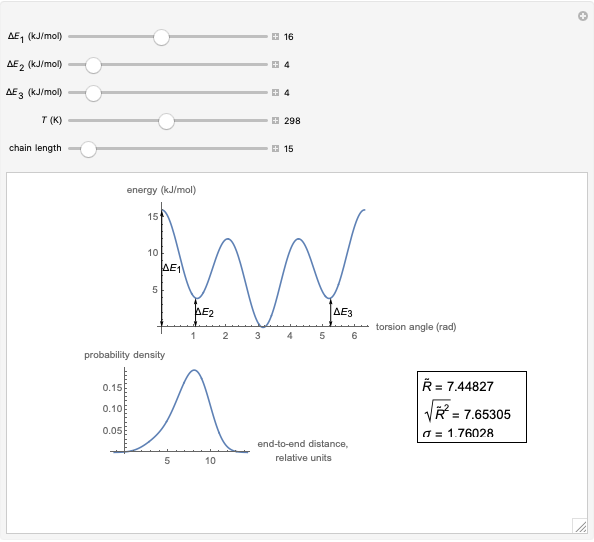
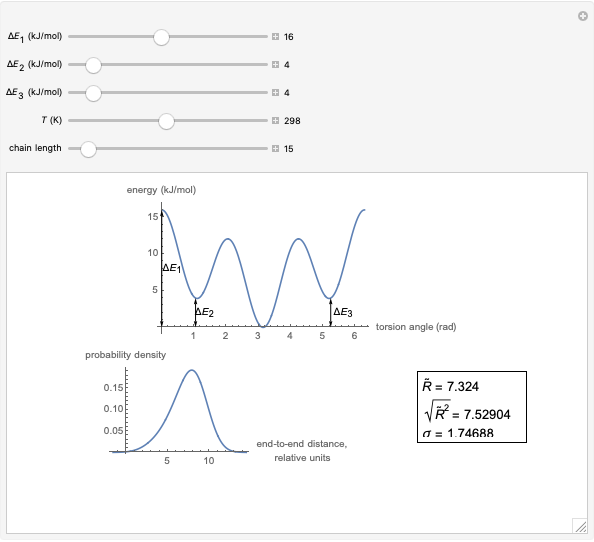
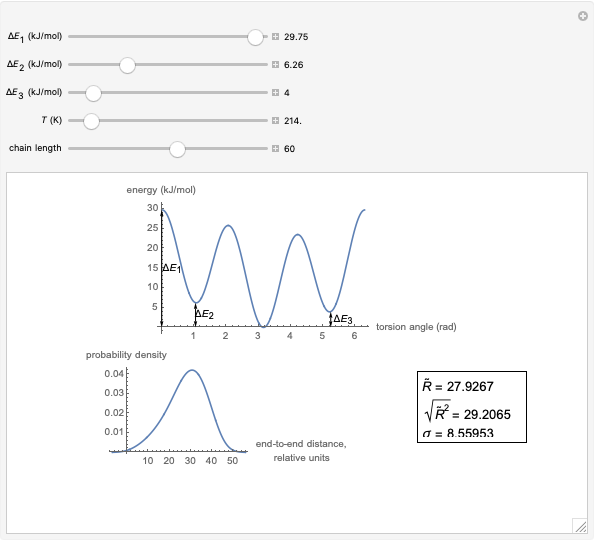
This Demonstration shows the dependence of the end-to-end distance distribution of a linear substituted polymethylene chain on energy barriers, temperature and chain length. The parameter values are automatically reset to force  and
and  .
.
Contributed by: A. A. Koledenkov (April 2019)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The conformational energy of hindered rotation  in a classical molecular mechanics simulation in the general case is approximated by the equation [1]:
in a classical molecular mechanics simulation in the general case is approximated by the equation [1]:
 .
.
The parameters  and
and  describe a force field with torsion angle
describe a force field with torsion angle  .
.
This Demonstration uses a modified version of the potential:

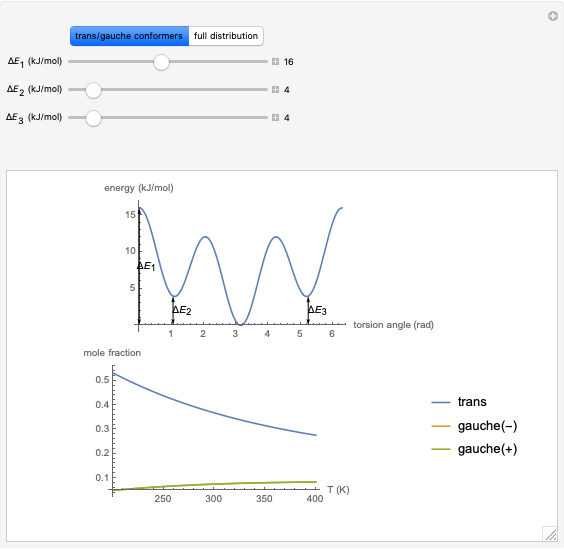
where  is the energy barrier (kJ/mol) and
is the energy barrier (kJ/mol) and  and
and  are the energy difference gauche(-)/trans and gauche(+)/trans conformers, respectively (kJ/mol).
are the energy difference gauche(-)/trans and gauche(+)/trans conformers, respectively (kJ/mol).
The effect of excluded volume is neglected in the calculation.
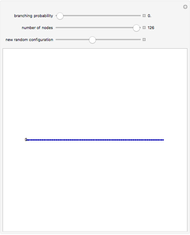
Using the Monte Carlo method, 500 macromolecular chains are generated. For a chain of length  ,
,  torsion angle values are generated. To simplify the calculation, selection of the torsion angle is performed taking into account the statistical weight based on the cumulative distribution function
torsion angle values are generated. To simplify the calculation, selection of the torsion angle is performed taking into account the statistical weight based on the cumulative distribution function  at temperature
at temperature  , divided into 36 equal intervals with step size 10°. This avoids the calculation of the Boltzmann factor for individual chains:
, divided into 36 equal intervals with step size 10°. This avoids the calculation of the Boltzmann factor for individual chains:
 .
.
For each chain, the end-to-end distance  is calculated. The distance is expressed in relative units of carbon-carbon bond length. For visualization, a smoothed function is used to exclude statistical scatter;
is calculated. The distance is expressed in relative units of carbon-carbon bond length. For visualization, a smoothed function is used to exclude statistical scatter;  values are the result of smoothing and should be ignored.
values are the result of smoothing and should be ignored.
Based on the distribution, the mean  , root mean square
, root mean square  , end-to-end distance and standard deviation
, end-to-end distance and standard deviation  are calculated:
are calculated:
 ,
,
 ,
,
 .
.
Reference
[1] M. Bachmann, Thermodynamics and Statistical Mechanics of Macromolecular Systems, Cambridge, UK: Cambridge University Press, 2014.
Permanent Citation