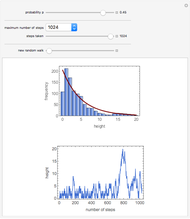
Distributions in Direction-Biased Random Walk
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
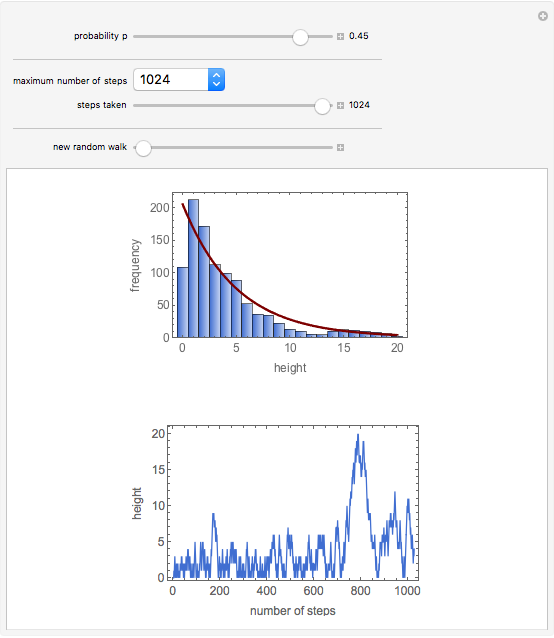
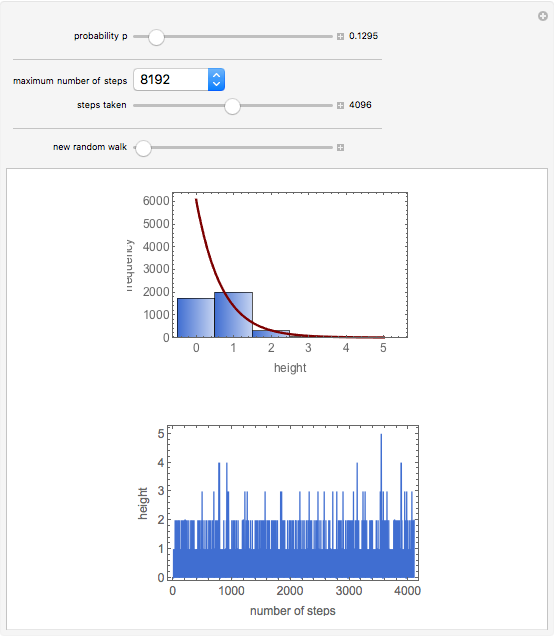
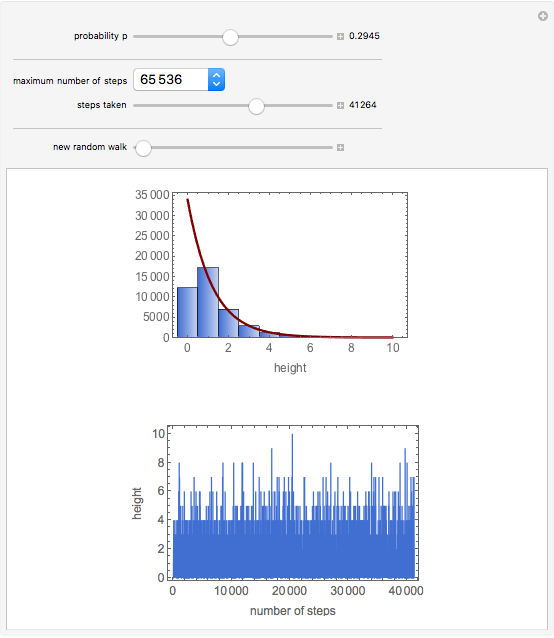
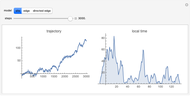
This Demonstration simulates a random walk that steps up with probability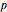 
and down with probability 
(
), but cannot step to negative values.
Contributed by: Simon Mochrie (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This simulation is a model for a particle undergoing Brownian motion subject to a constant force 
directed downward, but with an impenetrable barrier at zero. Force and probability are related via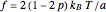 
, where 
is the step size, 
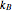is Boltzmann's constant, and 
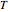is the absolute temperature.
The result might represent the height of a colloidal particle (i.e., a micron- or submicron-sized) in a beaker of water. It could also represent the height of a gas molecule in the Earth's atmosphere.
For a sufficiently long simulation, the distribution of particle positions (sufficiently far from zero) may be seen to be a negative exponential function of the height with a characteristic decay length of 
.
Permanent Citation
The Maxwell Speed Distribution
Jan Fiala
Random Walk and Diffusion of Many Independent Particles: An Agent-Based Simulation
Hiroki Sayama
Two-State Random Walk Distribution
John Cicilio
Generic Random Walk and Maximal Entropy Random Walk
Bartlomiej Waclaw
A Reluctant Random Walk
Heikki Ruskeepää
Self-Similarity in Random Walk
Hiroki Sayama
The "True" Self-Avoiding Random Walk in Z
Balint Veto, Budapest University of Technology and Economics (BME), Department of Stochastics
Properties of a Simple Random Walk with Boundaries
Peter Falloon
Mean-Reverting Random Walks
Jason Cawley
Polynomial Fits of Random Walks
Michael Schreiber
