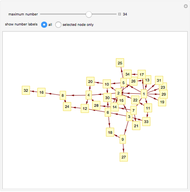
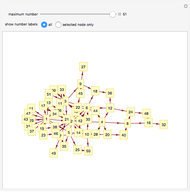
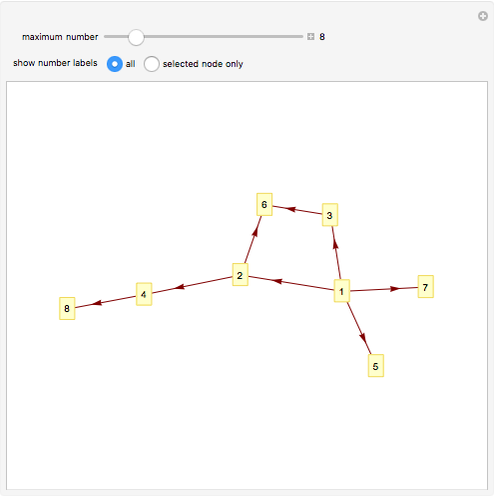
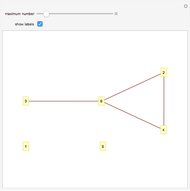
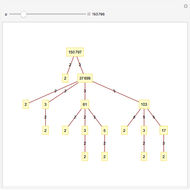
Divisibility Graph

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
An arrow is drawn from 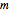 to
to  when (1)
when (1) 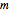 is a factor of
is a factor of  and (2)
and (2) 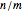 is prime. Consequently, there is a path of arrows from
is prime. Consequently, there is a path of arrows from 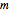 to
to  if and only if
if and only if 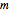 is a proper factor of
is a proper factor of  .
.
Contributed by: Don Goldberg (March 2011)
Based on a program by: Yifan Hu and Stephen Wolfram
Open content licensed under CC BY-NC-SA
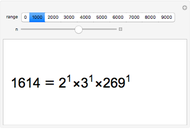
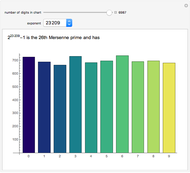
Snapshots
Details
The relation 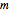 divides
divides  is a partial order: it is reflexive, antisymmetric, and transitive. These properties are expressed in the directed graphs generated here. Reflexivity: there is a path of (zero) arrows from each vertex to itself. Antisymmetry: if there is a path of arrows from
is a partial order: it is reflexive, antisymmetric, and transitive. These properties are expressed in the directed graphs generated here. Reflexivity: there is a path of (zero) arrows from each vertex to itself. Antisymmetry: if there is a path of arrows from 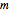 to
to  , there cannot be a path in the reverse direction. Transitivity: a path of arrows from
, there cannot be a path in the reverse direction. Transitivity: a path of arrows from 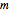 to
to  can be appended to a path of arrows from
can be appended to a path of arrows from  to
to 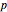 to create a path from
to create a path from 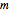 to
to 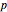 .
.
Permanent Citation